Stefania chiede: Esercizio asintoti

Pubblicato il da EdoLascia un commento
0

Una studentessa scrive:

Quando è necessario verificare l’esistenza dell’asintoto obliquo? Determinare l’equazione dell’asintoto obliquo per la seguente funzione:

y= \frac {5x^3-2x}{x^2-1}.

 

Risposta dello staff

Allora, affinchè esistano asintoti obliqui è NECESSARIO che non esistano gli asintoti orizzontali, ovvero che la funzione, all’infinito, tenda ad infinito:

y=\lim_{x \to \infty} f(x)= \infty

e poi dovranno esistere m e q tali che esistano e siano finiti i due limiti:

m=\lim_{x \to \infty} \frac {f(x)}{x} e

q=\lim_{x \to \infty} f(x)-mx.

Si ha subito, a prescindere dal segno, che:

y=\lim_{x \to \infty} \frac {5x^3-2x}{x^2-1}= \lim_{x \to \infty} \frac {x^3(5-2\frac {1}{x^2}}{x^2(1-\frac {1}{x^2}}=\lim_{x \to \infty} \frac {5x^3}{x^2}=5\lim_{x \to \infty} x=\infty.

Quindi proviamo a calcolare m:

m=\lim_{x \to \infty} \frac {f(x)}{x}=\lim_{x \to \infty} \frac {5x^3-2x}{x^2-1} \frac 1x =\lim_{x \to \infty} \frac {x^3(5-2\frac {1}{x^2}}{x^3(1-\frac {1}{x^2}}=\lim_{x \to \infty} \frac {5x^3}{x^3}=5.

Proviamo ora a calcolare q:

q=\lim_{x \to \infty} f(x)-mx=\lim_{x \to \infty} \frac {5x^3-2x}{x^2-1}-5x=\lim_{x \to \infty} \frac {5x^3-2x-5x^3+5x}{x^2-1}=\lim_{x \to \infty} \frac {3x}{x^2-1}=0,

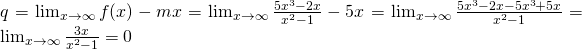perchè il denominatore è di grado superiore al numeratore.

Quindi l’asintoto obliquo sarà unico e avrà equazione:

y=5x.

 

 

 

(Questa pagina è stata visualizzata da 295 persone)

Lascia un commento