Sandra scrive: Esercizio equazione parametrica

Pubblicato il da EdoLascia un commento
-2

Una studentessa scrive

Corpo del messaggio:
12x^2-2(k-3)x-k=0

a) Una radice è tripla dell’ altra
b) Il rapporto tra le radici è 1/6

 

Risposta dello staff

 

Innanzitutto calcoliamo per quali valori di k l’equazione ammette soluzioni reali:

\Delta=4(k-3)^2+48k=4k^2-24k+36+48k=4k^2+24k+36=4(k^2+6k+9)=4(k+3)^2

Essendo un prodotto di due quadrati, sicuramente ammetterà soluzioni reali per ogni valore di k. Analizziamo ora le richieste:
a) Una radice è tripla dell’ altra

Noi sappiamo quindi, che:

3x_1=x_2

e che:

x_1+x_2=4x_1=\frac {2(k-3)}{12}=\frac 16 (k-3)

quindi:

x_1=\frac {1}{24}(k-3)

Sappiamo anche che:

x_1*x_2=3x_1^2=-\frac {1}{12}k

e quindi:

x_1^2=-\frac {1}{36}k

Mettendo a sistema otteniamo:

\begin{cases} x_1=\frac {1}{24} (k-3) \\ x_1^2=-\frac {1}{36}k \end{cases}

\begin{cases} x_1^2=\frac {1}{576} (k-3)^2 \\ x_1^2=-\frac {1}{36}k \end{cases}

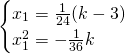
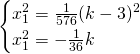
Analizziamo solo l’equazione finale:

\frac {1}{576} (k-3)^2 =-\frac {1}{36}k

(k-3)^2=-16k

k^2-6k+9+16k=0

k^2+10k+9=0

k_{\frac 12}=\frac {-10 \pm \sqrt {100-36}}{2}=\frac {-10 \pm \sqrt {64}}{2}=\frac {-10 \pm 8}{2}=-5 \pm 4

ovvero:

k_1= -9 \quad \wedge \quad k_2=-1
b) Il rapporto tra le radici è 1/6

Noi sappiamo quindi, che:

\frac {x_1}{x_2}=\frac 16

e quindi:

x_2=6x_1

Utilizzando lo stesso criterio di sopra, otteniamo:

x_1+x_2=7x_1=\frac {2(k-3)}{12}=\frac 16 (k-3)

quindi:

x_1=\frac {1}{42}(k-3)

Sappiamo anche che:

x_1*x_2=6x_1^2=-\frac {1}{12}k

e quindi:

x_1^2=-\frac {1}{72}k

Mettendo a sistema otteniamo:

\begin{cases} x_1=\frac {1}{42} (k-3) \\ x_1^2=-\frac {1}{72}k \end{cases}

\begin{cases} x_1^2=\frac {1}{1764} (k-3)^2 \\ x_1^2=-\frac {1}{72}k \end{cases}

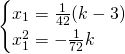
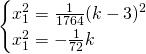
Analizziamo solo l’equazione finale:

\frac {1}{1764} (k-3)^2 =-\frac {1}{72}k

2(k-3)^2=-49k

2k^2-12k+18+49k=0

2k^2+37k+18=0

k_{\frac 12}=\frac {-37 \pm \sqrt {1369-144}}{4}=\frac {-37 \pm \sqrt {1225}}{4}=\frac {-37 \pm 35}{4}

ovvero:

k_1= -18 \quad \wedge \quad k_2=-\frac 12

 

 

 

(Questa pagina è stata visualizzata da 179 persone)

Lascia un commento