Eleonora scrive: Aiuto esercizi

Pubblicato il da EdoLascia un commento
0

Corpo del messaggio:
1) Trovare le coordinate dei punti intersezione della retta r passante per i seguenti punti:

A = (10,00 ; -27,00)

B = ( -20,00 ; 33,00)

e la parabola di equazione y= -x^2 -8

2) Risolvere il seguente sistema di disequazioni

\begin {cases} \frac {2x^2 -5x -3}{ 4x -1} \geq 0 \\ x^2 -7x +6 \geq 0 \end {cases}

 

 

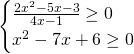
Risposta dello staff

Per trovare la retta passante per quei due punti, basterà sfruttare l’equazione:

\frac {y-y_A}{y_B-y_A}=\frac {x-x_A}{x_B-x_A}

sostituendo i valori delle incognite

\frac {y+27}{33+27}=\frac {x-10}{-20-10}

\frac {y+27}{60}=\frac {x-10}{-30}

y+27=-2x+20

y=-2x-7

Mettiamo ora a sistema la retta con la parabola:

\begin{cases} y=-2x-7 \\ y= -x^2-8\end{cases}

\begin{cases} y=-2x-7 \\ -2x-7= -x^2-8\end{cases}

\begin{cases} y=-2x-7 \\ x^2-2x+1= 0\end{cases}

\begin{cases} y=-2x-7 \\ (x-1)^2= 0\end{cases}

\begin{cases} y=-2x-7 \\ x= 1\end{cases}

\begin{cases} y=-2-7=-9 \\ x= 1\end{cases}

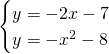
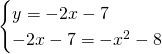
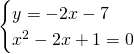
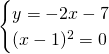
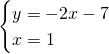
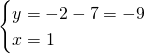
Quindi avrà un unico punto di intersezione:

C(1,-9)

2) Risolvere il seguente sistema di disequazioni

\begin {cases} \frac {2x^2 -5x -3}{ 4x -1} \geq 0 \\ x^2 -7x +6 \geq 0 \end {cases}

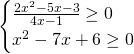
Analizziamo ogni singola disequazione:

  • 2x^2-5x-3 \geq0

Le due soluzioni saranno:

x_{\frac 12}= \frac {5 \pm \sqrt {25+24}}{4}=\frac {5 \pm \sqrt {49}}{4}=\frac {5 \pm 7}{4}

Quindi:

x_1=-\frac 12

x_2= 3

La disequazione sarà quindi verificata per :

x \leq -\frac 12 \quad \lor \quad x \geq 3

  • 4x-1 >0

x > \frac 14

-\frac 12 \frac14 3
++++ — — — — — ++++
— — — — ++++ ++++ ++++
— ++++ ++++ ++++ — — ++++

 

La fratta sarà quindi verificata per

-\frac 12 \leq x < \frac 14 \quad \lor \quad x \geq 3

  • x^2-7x+6 \geq 0

Le due soluzioni saranno:

x_{\frac 12}= \frac {7 \pm \sqrt {49-24}}{2}=\frac {7 \pm \sqrt {25}}{2}=\frac {7 \pm 5}{2}

Quindi:

x_1=1

x_2= 6

La disequazione sarà quindi verificata per :

x \leq 1 \quad \lor \quad x \geq 6

Mettiamo tutto a sistema per ottenere:

\begin{cases} -\frac 12 \leq x < \frac 14 \quad \lor \quad x \geq 3 \\x \leq 1 \quad \lor \quad x \geq 6 \end{cases}

-\frac12 \frac 14 1 3 6
++++ ++++ ++++ ++++ ++++
++++ ++++ ++++ ++++ ++++ ++++
++++ ++++ ++++ ++++

 

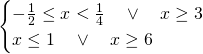
La soluzione finale sarà:

-\frac 12 \leq x < \frac 14 \quad \lor \quad x \geq 6

 

 

 

(Questa pagina è stata visualizzata da 220 persone)

Lascia un commento