Annamaria scrive: Esercizio triangoli simili

Una studentessa scrive:

Oggetto: problema di geometria..help!!!

Corpo del messaggio:
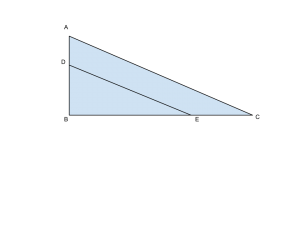
nel triangoloABC, rettangolo inB, una parallela ad AC interseca nel punto D e BC in E, con 5AD=2BE. Sapendo che EC supera di 4 cm gli 8/15 di EB e che BD è lungo cm 5 meno dei 3/4 di EB, detrmina l’areadel triangolo BDE.

Risposta dello staff

Dai dati abbiamo che:

$5AD=2BE$

$EC=4+\frac {8}{15}EB$

$BD=\frac 34 EB-5$

Denotiamo $EB=x$ e otteniamo:

$AD=\frac 25 x$

$EC=4+\frac {8}{15}EB$

$BD=\frac 34 x -5$

Dato che i due triangoli sono simili, possiamo eseguire la proporzione:

$BE:BC=BD:AB$

sapendo che:

$AB=AD+DB=\frac 25 x + \frac 34 x -5=\frac {23x-100}{20}$ ,

$BC=BE+EC=x+4+\frac {8}{15}x=\frac {23x+60}{15}$ .

Ora avremo:

$\frac {x}{\frac {23x+60}{15}}= \frac {\frac {3x-20}{4}}{\frac {23x-100}{20}}$

$\frac {15x}{23x+60}=\frac {15x-100}{23x-100}$

$345x^2-1500x=345x^2+900x-2300x-6000$

$-1500x=-1400x-6000$

$-100x=-6000$

$x=60$

Quindi avremo:

$BE= 60 \mbox { cm}$

$BD=40 \mbox { cm}$

Con questi due dati possiamo ricavare l’area del triangolo BDE:

$A_{BDE}= \frac {BD \cdot BE}{2}= \frac {40 \cdot 60}{2} \mbox { cm}^2=1200 \mbox { cm}^2$

(Questa pagina è stata visualizzata da 194 persone)

Matebook

La matematica spiegata passo passo

Annamaria scrive: Esercizio triangoli simili

Risposta dello staff

Lascia un commento Annulla risposta