Erica scrive: Esercizio integrale

Oggetto: soluzione di un esercizio

Corpo del messaggio:
ciaoo questo è l’esercizio :

$\int \frac {\mathrm {d} x}{\sqrt{1 + e^{3x}}}$

mandami la soluzione alla mia email grazie.

Svolgimento

Questo integrale va effettuato per sostituzione.

Poniamo:

$\sqrt{1 + e^{3x }}=t$

$1+e^{3x}=t^2$

$e^{3x}=t^2-1$

$3x=log (t^2-1)$

$x= \frac 13 log(t^2-1)$

$\mathrm{d} x= \frac 13 \frac {2t}{t^2-1} \mathrm{d}t$

Sostituendo tutto nell’integrale iniziale otteniamo:

$\int \frac {\frac {2t}{3(t^2-1)}}{t} \mathrm{d}t=$

$\int \frac {2}{3(t^2-1)} \mathrm{d}t=$

$\frac 23 \int \frac {1}{t^2-1} \mathrm{d}t$ .

Ora consideriamo solo la frazione all’interno e avremo:

$\frac {1}{t^2-1}=\frac {1}{(t+1)(t-1)}= \frac {A}{t+1}+ \frac {B}{t-1}=\frac {At-A+Bt+B}{t^2-1}=\frac {(A+B)t+B-A}{t^2-1}$

Da qui avremo che:

$\begin {cases} A+B=0 \\ B-A=1\end {cases}$

$\begin {cases} B=\frac 12 \\ A=-\frac 12\end {cases}$

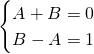
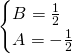
Ritornando quindi all’integrale otteniamo:

$\frac 23 \int \left( \frac {- \frac 12 }{t+1} + \frac {\frac 12}{t-1} \right)\mathrm{d}t=$

$\frac 23 (\frac 12)\int \left( -\frac { 1 }{t+1} + \frac {1}{t-1} \right)\mathrm{d}t=$

$\frac 13 (-log (t+1)+ log(t-1))+c=$

$\frac 13 log \frac {t-1}{t+1}+c$

Sostituire infine l’incognita iniziale:

$\frac 13 log \frac {\sqrt{1 + e^{3x }}-1}{\sqrt{1 + e^{3x }}+1}+c$

(Questa pagina è stata visualizzata da 141 persone)

Matebook