Francesco scrive: Esercizio integrali

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: SOLUZIONE DI UN ESERCIZIO

Corpo del messaggio:
ciao vorrei sapere come si risolve questo: integrale 3x -2 fratto ( x-1).(x^2 -2x+2)

 

Risposta dello staff

\int \frac {3x-2}{(x-1)(x^2-2x+2)} \, dx

Basterà ricordarsi della formula degli integrali delle funzioni razionali:

\frac {3x-2}{(x-1)(x^2-2x+2)}=\frac {A}{x-1}+ \frac {Bx+C}{x^2-2x+2}=\frac {Ax^2-2Ax+2A+Bx^2-Bx+Cx-C}{(x-1)(x^2-2x+2)}=\frac {x^2(A+B)-x(2A+B-C)+2A-C}{(x-1)(x^2-2x+2)}

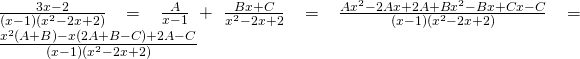
Da qui avremo:

\begin{cases} A+B=0 \\ 2A+B-C=-3 \\ 2A-C=-2\end{cases}

\begin{cases} A+B=0 \\ B-2=-3 \\ C=2A+2\end{cases}

\begin{cases} A=1 \\ B=-1 \\ C=4\end{cases}.

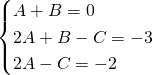
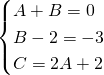
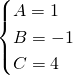Così l’integrale diventa:

\int \frac {3x-2}{(x-1)(x^2-2x+2)} \, dx = \int \frac {1}{x-1} \, dt + \int \frac {-x+4}{x^2-2x+2} \, dt=

Il primo è un integrale immediato, mentre nel secondo moltiplichiamo e dividiamo per 2 in modo da ottenere la derivata del denominatore al numeratore:

log(x-1) -\frac 12 \int \frac {2x-8}{x^2-2x+2} \, dt=log(x-1) -\frac 12 \int \frac {2x-2-6}{x^2-2x+2} \, dt.

Ora separiamo le due frazioni così da avere integrali immediati:

log(x-1) -\frac 12 \int \frac {2x-2-6}{x^2-2x+2} \, dt=log(x-1) -\frac 12 \int \frac {2x-2}{x^2-2x+2} \, dt - \frac 12 \int \frac {-6}{x^2-2x+2} \, dt=

log(x-1) -\frac 12 log(x^2-2x+2) +3\int \frac {1}{x^2-2x+1+1} \, dt=

log(x-1) -\frac 12 log(x^2-2x+2) +3\int \frac {1}{1+(x-1)^2} \, dt=

log(x-1) -\frac 12 log(x^2-2x+2) +3arctg(x-1)+c

 

 

 

(Questa pagina è stata visualizzata da 139 persone)

Lascia un commento