Corpo del messaggio:
ciao ti chiedo gentilmente la soluzione di questo esercizio: integrale di dx fratto e^2x-3e^x+2 e anche integrale di e^x fratto 3e^2x- e^x+2 grazie
1) ![]()
Utilizziamo il criterio di sostituzione e otteniamo:
![]()
![]()
![]()
Sostituendo otteniamo:
![]()
![]()
Utilizziamo la formula per gl integrali di funzioni razionali:
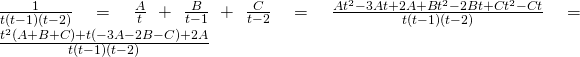
Risolviamo il sistema:
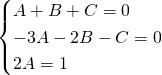
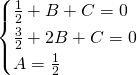
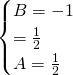 .
.
Quindi l’integrale diventa:
![]()
![]()
![]()
(Questa pagina è stata visualizzata da 120 persone)