Nicolò scrive: Esercizio sistemi di disequazioni

Oggetto: sistemi di disequazioni

Corpo del messaggio:

Risolviamo il primo sistema:

$\begin{cases} \frac {x-2}{x+3}\geq 0\\ 7+2x>-\frac {x^2}{7} \end{cases}$

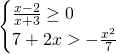
Per la prima disequazione discutiamo numeratore e denominatore ottenendo:

Avremo quindi:

$\begin{cases} x < -3 \quad \lor \quad x \geq 2 \\ x^2+14x +49 >0 \end{cases}$

$\begin{cases} x < -3 \quad \lor \quad x \geq 2 \\ (x+7)^2 >0 \end{cases}$

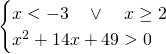
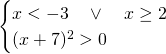
La seconda disequazione è verificata sempre a meno di $x=7$ .

Avremo quindi:

$\begin{cases} x < -3 \quad \lor \quad x \geq 2 \\ x \neq 7 \end{cases}$

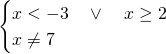
Che risulterà anche essere la soluzione del sistema iniziale:

$x<-3 \quad \lor \quad x \geq 2 \mbox { con } x \neq 7.$

Secondo sistema:

$\begin{cases} (x+1)^2 \leq 16 \\ x(x-7) \geq 4(5-2x)\end{cases}$

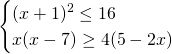
Sulla prima sfruttiamo una particolarità delle disequazioni di secondo grado, ovvero:

$y^2 \leq a^2 \iff -a \leq y \leq a$ , così da avere:

$\begin{cases} -4 \leq x+1 \leq 4 \\ x^2-7x \geq 20-8x\end{cases}$

$\begin{cases} -5 \leq x \leq 3 \\ x^2+x-20 \geq 0\end{cases}$

$\begin{cases} -5 \leq x \leq 3 \\ (x-4)(x+5) \geq 0\end{cases}$

$\begin{cases} -5 \leq x \leq 3 \\ x \leq -5 \quad x \geq 4\end{cases}$

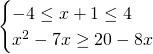
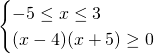
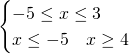
Come notiamo dalle soluzioni, questo sistema ammette come soluzione solo $x=-5$

(Questa pagina è stata visualizzata da 105 persone)

Matebook