Francesco scrive: Esercizio sistema di disequazioni

Oggetto:

Corpo del messaggio:

$\begin{cases} \frac{\left|x-1\right|-\left|x\right|}{2-\sqrt[3]{x+4}}<0 \\\frac {\sqrt{6-x}-6+4x}{2x-2+\sqrt{9-x}} \leq 0 \end{cases}$

Studiamo separatamente i casi:

numeratore prima frazione

$\left|x-1\right| - \left| x \right| >0$

Avremo 3 sistemi:

$\begin{cases} x<0 \\ 1-x+x>0\end{cases} \quad \begin{cases} 0\leq x\leq 1 \\ 1-x-x>0\end{cases} \quad \begin{cases} x>1 \\ x-1-x>0\end{cases}$

$\begin{cases} x<0 \\ 1>0\end{cases} \quad \begin{cases} 0\leq x\leq 1 \\ x<\frac 12\end{cases} \quad \begin{cases} x>1 \\ -1>0\end{cases}$

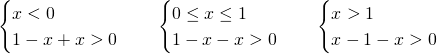
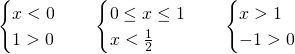
I sistemi avranno come soluzione:

$x<0$
$x<\frac 12$
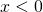
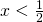
impossibile

Unendo quindi il numeratore sarà verificato per $x<\frac 12$

denominatore prima frazione

$2-\sqrt[3]{x+4}>0$

$\sqrt[3]{x+4}<2$

$x+4<8$

$x<4$

La prima frazione quindi sarà verificata per $\frac 12 <x<4$ .

Analizziamo i termini della seconda frazione

numeratore seconda frazione:

$\sqrt{6-x}-6+4x \geq 0$

$\sqrt{6-x}\geq 6-4x$

Svolgiamo due sistemi e uniamo le soluzioni:

$\begin{cases} 6-4x <0 \\ 6-x \geq 0\end{cases} \quad \begin{cases} 6-4x \geq 0 \\ 6-x \geq (6-4x)^2\end{cases}$

$\begin{cases} x >\frac 32 \\ x \leq 6\end{cases} \quad \begin{cases} x \leq \frac 32 \\ 6-x \geq 36-48x+16x^2\end{cases}$

$\begin{cases} x >\frac 32 \\ x \leq 6\end{cases} \quad \begin{cases} x \leq \frac 32 \\ 16x^2-47x+30 \leq 0\end{cases}$

$\begin{cases} x >\frac 32 \\ x \leq 6\end{cases} \quad \begin{cases} x \leq \frac 32 \\ \frac {15}{16}\leq x \leq 4 \end{cases}$

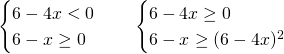
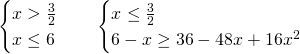
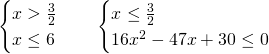
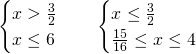
I sistemi avranno come soluzione:

$\frac 32 < x \leq 6$
$\frac {15}{16}\leq x\leq \frac 32$

Unendo le due il sistema sarà verificato per $\frac {15}{16}\leq x \leq 6$

denominatore seconda frazione

$2x-2+\sqrt{9-x}>0$

$\sqrt{9-x}>2-2x$

Svolgiamo due sistemi e uniamo le soluzioni:

$\begin{cases} 2-2x <0 \\ 9-x \geq 0\end{cases} \quad \begin{cases} 2-2x \geq 0 \\ 9-x > (2-2x)^2\end{cases}$

$\begin{cases} x > 1 \\ x \leq 9\end{cases} \quad \begin{cases} x \leq 1 \\ 9-x > 4-8x+4x^2\end{cases}$

$\begin{cases} x > 1 \\ x \leq 9\end{cases} \quad \begin{cases} x \leq 1 \\ 4-8x+4x^2+x-9<0\end{cases}$

$\begin{cases} x > 1 \\ x \leq 9\end{cases} \quad \begin{cases} x \leq 1 \\ 4x^2-7x-5<0\end{cases}$

$\begin{cases} x > 1 \\ x \leq 9\end{cases} \quad \begin{cases} x \leq 1 \\ \frac {7 - \sqrt {129}}{8}<x<\frac {7+\sqrt {129}}{8}\end{cases}$

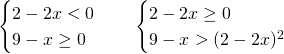
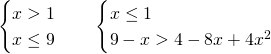
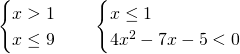
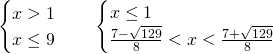
I sistemi avranno come soluzione:

$1 < x \leq 9$
$\frac {7-\sqrt{129}}{8}< x\leq 1$

Unendo le due il sistema sarà verificato per $\frac {7-\sqrt{129}}{8}< x\leq 9$

Mettendo insieme i risultati dei due fattori, la seconda disequazione sarà verificata per $\frac {7-\sqrt{129}}{8}< x\leq \frac {15}{16}$ . Escludiamo la possibilità di $x>9$ in quanto renderebbe privo di significato il numeratore.

Mettendo a sistema:

$\begin{cases}\frac 12 <x<4 \\ \frac {7-\sqrt{129}}{8}< x\leq \frac {15}{16} \end{cases}$ ,

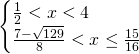avremo che la soluzione finale è:

$\frac 12< x\leq \frac {15}{16}$

(Questa pagina è stata visualizzata da 151 persone)

Matebook

La matematica spiegata passo passo

Francesco scrive: Esercizio sistema di disequazioni

Lascia un commento Annulla risposta