Cesare scrive: Esercizio disequazioni irrazionali

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Disequazioni Irrazionali

Corpo del messaggio:
Buona sera,
Avrei bisogno di sapere perche i miei esercizi che hanno soluzioni “tutte” o “nessuna x appartenente a R” non mi vengono. Credo che io stia facendo un errore quando disegno i grafici con tutte o nessuna x appartenente a r e con un x>n o x<n!

Grazie mille e complimenti per il sitoweb!

Untitled

 

Analizziamo il primo caso:

\sqrt {3-x}> x-3

\begin{cases} x-3<0 \\ 3-x \geq 0 \end{cases} \quad \lor \quad \begin{cases} x-3\geq 0 \\ 3-x > x^2-6x+9\end{cases}

\begin{cases} x<3 \\ x \leq 3 \end{cases} \quad \lor \quad \begin{cases} x\geq 3 \\ x^2-5x+6<0\end{cases}

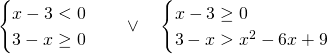
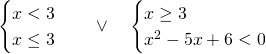
Il primo sistema è facilmente verificabile per x<3, mentre nel secondo hai sbagliato qualcosa:

x^2-5x+6<0

Le soluzioni sono: x_{\frac 12}=\frac {5\pm 1}{2}, quindi x_1=2 e x_2=3. Da cui la soluzione della disequazione è 2<x<3, che non ha soluzioni comuni con x\geq 3.

Rimane quindi solo la soluzione del primo sistema.

 

Analizziamo il secondo caso:

senza bisogno di fare tutti i calcoli, hai sbagliato sul primo sistema.

Nel momento in cui tu vai a calcolare x^2+2x+9 \geq 0, e il \Delta, come hai calcolato, è negativo, questa disequazione è verificata per ogni valore dell’incognita…

Quando non sei sicuro dei risultati prova a sostituire al posto della x un numero qualsiasi…

Esempio:

Se x valesse 0, x^2+2x+9=0+0+9 che è un numero positivo; stesso discorso vale per qualsiasi numero tu vada a sostituire.

Un consiglio per le prossime volte in cui incontri un \Delta negativo, e non sei sicuro del risultato della disequazione associata: sostituisci 0 all’incognita e vedi se esce un valore positivo o negativo; tutti gli altri valori assumeranno lo stesso segno!!!

(Questa pagina è stata visualizzata da 112 persone)

Lascia un commento