Franco scrive: Esercizio di trigonometria

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Esercizio trigonometria

Corpo del messaggio:
sapendo che cosx=-1/4 con 90°<x<180°, calcola tan(2x+pgreco/3)

 

Riscriviamo meglio:

 

tan(2x+\frac {\pi}{3})=\frac {tan(2x)+tan\left(\frac {\pi}{3}\right)}{1-tan(2x)tan\left(\frac {\pi}{3}\right)}=\frac {tan(2x)+\sqrt 3 }{1-\sqrt 3tan(2x)}

Sappiamo che:

tg(2x)=\frac {2tgx}{1-tg^2x},

e quindi sostituendo otteniamo:

\frac {\frac {2tgx}{1-tg^2x}+\sqrt 3 }{1-\sqrt 3\frac {2tgx}{1-tg^2x}}.

Sapendo il valore del coseno, ricaviamo il valore del seno che, nel quadrante considerato sarà positivo:

senx=\sqrt {1-cos^2x}=\sqrt {1-\frac {1}{16}}=\sqrt {\frac {15}{16}}=\frac {\sqrt {15}}{4}.

Quindi avremo che la tangente sarà:

tgx=\frac {senx}{cosx}=\frac {\frac {\sqrt {15}}{4}}{-\frac 14}=-\sqrt {15}

Sostituiamo nell’espressione iniziale così da ottenere:

\frac {\frac {-2\sqrt{15}}{1-15}+\sqrt 3 }{1+\sqrt 3\frac {2\sqrt {15}}{1-15}}=\frac {\frac {\sqrt{15}}{7}+\sqrt 3 }{1 - \frac {3\sqrt {5}}{7}}=\frac {\sqrt {15}+ 7\sqrt 3}{7} \frac {7}{7-3\sqrt 5}=\frac {\sqrt {15}+7\sqrt 3}{7-3\sqrt 5}=\frac {\sqrt {15}+7\sqrt 3}{7-3\sqrt 5}\frac {7+3\sqrt 5}{7+3\sqrt 5}=\frac {7\sqrt {15}+15\sqrt 3+49\sqrt 3+21\sqrt {15}}{49-45}=\frac {64\sqrt 3+28\sqrt 15}{4}=16\sqrt 3 + 7\sqrt {15}.

 

 

 

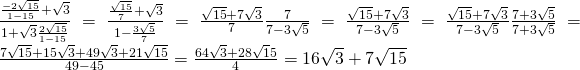(Questa pagina è stata visualizzata da 110 persone)

Lascia un commento