Oggetto: Come si risolve questa Equazione con radici?
Corpo del messaggio:
Risposta dello staff
![]()
Non essendoci la richiesta per questo esercizio, suppongo la richiesta sia di verificare ove questa funzione possa essere verificata, ovvero, calcolare per quali valori di x esista un valore della y.
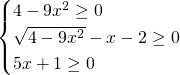
Studiamo separatamente i casi:
![]()
Le due soluzioni dell’equazione associata sono: ![]() , e quindi la disequazione è verificata per:
, e quindi la disequazione è verificata per:
![]()
![]()
![]()
Analizziamo i due sistemi:
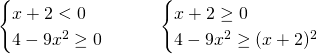
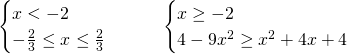


Quindi, il primo sistema non è mai verificato; il secondo sarà verificato per:
![]() .
.
Riportiamo tutto nel primo sistema:
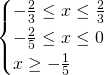
Mettendo tutto a sistema, notiamo che i tre pezzi saranno verificati per:
![]()
(Questa pagina è stata visualizzata da 146 persone)
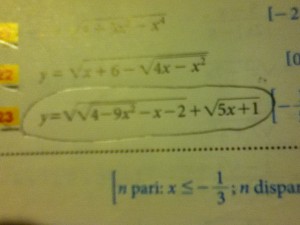
grazie mille