Matteo scrive: Esercizio sistema di equazioni

Pubblicato il da Lo StaffLascia un commento
0

Oggetto:

Corpo del messaggio:
-2/3 (x+y)-2 (y-4)=-5
1/3x +3/2z =y-1
3(x-z)=x+y
È un sistema a tre incognite potete risolvere con o il metodo di Cramer o sostituzione

 

Risposta dello staff

\begin{cases} -\frac 23 (x+y)-2 (y-4)=-5 \\ \frac 13 x +\frac 32 z =y-1 \\ 3(x-z)=x+y\end{cases}

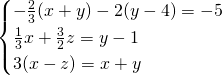
Sostituiamo subito dalla terza il risultato di x+y:

\begin{cases} -\frac 23 3(x-z)-2 (y-4)=-5 \\ \frac 13 x +\frac 32 z =y-1 \\ 3(x-z)=x+y\end{cases}

\begin{cases} 2(x-z)+2 (y-4)=5 \\ 2x +9 z =6y-6 \\ 3x-3z=x+y\end{cases}

\begin{cases} 2x-2z+2 y-8=5 \\ 2x -6y+9 z =-6 \\ 2x-y-3z=0\end{cases}

\begin{cases} 2x+2y-2z=13 \\ 2x -6y+9 z =-6 \\ 2x-y-3z=0\end{cases}

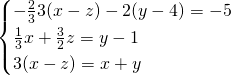
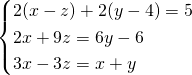
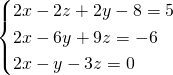
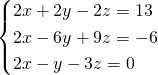
Sottriamo la seconda e la terza dalla prima, così da ottenere:

\begin{cases} 2x+2y-2z=13 \\ 8y-11 z =19 \\ 3y+z=13\end{cases}

\begin{cases} 2x+2y-2z=13 \\ 8y-11 (13-3y) =19 \\ z=13-3y\end{cases}

\begin{cases} 2x+2y-2z=13 \\ 8y-143+33y =19 \\ z=13-3y\end{cases}

\begin{cases} 2x+2y-2z=13 \\ 41y =162 \\ z=13-3y\end{cases}

\begin{cases} 2x+2y-2z=13 \\ y =\frac {162}{41} \\ z=13-3\frac {162}{41}\end{cases}

\begin{cases} 2x=13+2z-2y \\ y =\frac {162}{41} \\ z=\frac {533-486}{41}\end{cases}

\begin{cases} x=13+\frac {94}{41}-\frac{324}{41} \\ y =\frac {162}{41} \\ z=\frac {47}{41}\end{cases}

\begin{cases} x=\frac{533+94-324}{41} \\ y =\frac {162}{41} \\ z=\frac {47}{41}\end{cases}

\begin{cases} x=\frac{303}{41} \\ y =\frac {162}{41} \\ z=\frac {47}{41}\end{cases}

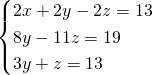
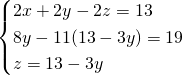
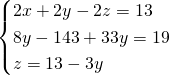
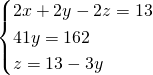
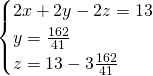
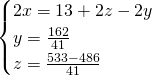
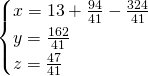
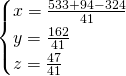
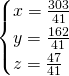
MA LA TRACCIA E’ GIUSTA???

 

 

(Questa pagina è stata visualizzata da 102 persone)

Lascia un commento