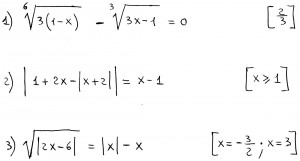Oggetto: Equazioni irrazionali e con moduli
Corpo del messaggio:
Per l’esercizio n. 1 allegato chiedo che venga svolto con le condizioni di esistenza e non con la verifica delle soluzioni.
Distinti saluti
Essendoci una radice di indice pari, svolgeremo il sistema, imponendo come condizione la positività del radicando stesso:
![Rendered by QuickLaTeX.com \[\begin{cases} \sqrt[6]{3(1-x)}=\sqrt[3]{3x-1} \\ 3(1-x) \geq 0\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-2700f5e67f5363a5f42e190649dcd4ee_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 3(1-x)=(3x-1)^2 \\ x \leq 1\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-dbd8866f9b22299d597a6214ed121fab_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 3-3x=9x^2-6x+1 \\ x \leq 1\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-008d5328bff6b696edfd7c6bdb478033_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 9x^2-3x-2=0 \\ x \leq 1\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-503ed22ef1e880d8f726cb9ab750d980_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x_{\frac 12}=\frac {3 \pm \sqrt {9+72}}{18} \\ x \leq 1\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-97f6056ff8c9e4e102857cf26e7f9995_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x_{\frac 12}=\frac {3 \pm \sqrt {81}}{18} \\ x \leq 1\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-401513160eb31983510fc49a5af81cd2_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x_{\frac 12}=\frac {3 \pm 9}{18} \\ x \leq 1\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-e5eea5478570ed6315ac68f5c770b722_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x_1=-\frac 13 \quad x_2=\frac 23 \\ x \leq 1\end{cases}.\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-37b381203a5a3933d873a8ddb06b378b_l3.png)
La prima soluzione è ovviamente da scartare in quanto, essendo la radice di indice dispari portatrice del segno (ovvero radice di segno positivo rimane positiva, e radice di segno negativo, rimane negativa, dobbiamo imporre come condizione iniziale che, essendoci una differenza, anche il radicando della radice cubica sia positivo. Avremo così:
![Rendered by QuickLaTeX.com \[\begin{cases} x_1=-\frac 13 \quad x_2=\frac 23 \\ x \leq 1 \\ x geq 13\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-cb3f0f6050b60a7e39409d7e987918d8_l3.png)
che darà come soluzione solo ![]() .
.
Distinguiamo subito due sistemi:
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq -2 \\ \left| 1+2x - x-2 \right| =x-1 \end{cases} \quad \quad \begin{cases} x < -2 \\ \left| 1+2x +x+2 \right| =x-1 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-a3e5708b727c2b2fc7d67acde275ccfb_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq -2 \\ \left| x-1 \right| =x-1 \end{cases} \quad \quad \begin{cases} x < -2 \\ \left| 3x +3 \right| =x-1 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-e8248708949a9bcf96b17d2b3de49b94_l3.png)
Dai due sistemi si potrebbe intuire subito la soluzione, ma svolgiamo prima i calcoli, notando che dovremmo avere due sistemi per ogni sistema creato:
- primo sistema:
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq -2 \\ x \geq 1 \\ x-1 =x-1 \end{cases} \quad \quad \begin{cases} x \geq -2 \\ x < 1 \\1-x =x-1 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-167d71bfc083e3ff712e7e3c2c3e07ac_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 1 \\ 0x =0 \end{cases} \quad \quad \begin{cases} -2 \leq x < 1 \\x =1 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-91a71a3750eba5569e1e405875733c04_l3.png)
Il primo sistema quindi ammetterà come soluzione ![]() , mentre il secondo sarà impossibile.
, mentre il secondo sarà impossibile.
- secondo sistema:
![Rendered by QuickLaTeX.com \[\begin{cases} x < -2 \\ x \geq -1 \\ 3x +3 =x-1 \end{cases} \quad \quad \begin{cases} x < -2 \\ x < -1 \\ -3x -3 =x-1 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-74d53ff38bb3f7252f795a8dfd9e5f65_l3.png)
Si vede subito che il primo sistema è impossibile; analizziamo solo il secondo:
![Rendered by QuickLaTeX.com \[\begin{cases} x < -2 \\ -4x =2 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-5de2f95af7f61b85f02e366da509ab62_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x < -2 \\ x =-\frac 12 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-69fa3bb7e684acef8051c284bc0940f1_l3.png)
quindi è impossibile anche il secondo.
L’equazione iniziale sarà quindi verificata per ogni ![]() .
.
Notiamo subito che, in questo caso, studiare la positività del radicando, è superfluo, essendo un modulo sempre positivo per definizione, e che il secondo termine sarà anch’esso sempre positivo, in quanto il minimo valore che potrà assumere, qualore l’incognita fosse positiva sarà 0.
Quindi avremo semplicemente che:
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ 2x-6 =0\end{cases} \quad \quad \begin{cases} x <0 \\ 6-2x=4x^2\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-3a604db3f0137054285e0136521510e9_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ x =3\end{cases} \quad \quad \begin{cases} x <0 \\ 4x^2+2x-6=0\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-4c79e62dc7851eac76b35bb552c6f148_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ x =3\end{cases} \quad \quad \begin{cases} x <0 \\ 2x^2+x-3=0\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-0e0722b67b27ab61659bf5b32dc2dd96_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ x =3\end{cases} \quad \quad \begin{cases} x <0 \\ x_{\frac 12}=\frac {-1 \pm \sqrt {1+24}}{4}\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-c6e6b6d2c05c35f75395efaa41f734e6_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ x =3\end{cases} \quad \quad \begin{cases} x <0 \\ x_{\frac 12}=\frac {-1 \pm \sqrt {25}}{4}\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-3c7407d2ed54b9a0b68dc99372a87e24_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ x =3\end{cases} \quad \quad \begin{cases} x <0 \\ x_{\frac 12}=\frac {-1 \pm 5}{4}\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-c21a9eff67ba318d6615600b29595366_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ x =3\end{cases} \quad \quad \begin{cases} x <0 \\ x_1=-\frac 32 \quad x_2=1\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-62f30870897b6e7cf8560ada3133392b_l3.png)
Il primo sistema sarà verificato per ![]() , mentre il secondo sarà verificato solo per
, mentre il secondo sarà verificato solo per ![]() .
.
(Questa pagina è stata visualizzata da 163 persone)