Luca scrive: Esercizio di geometria

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Geometria analitica . PER DMN

Corpo del messaggio:
Ecco gli esercizi sono a risposta multipla , mi dovete spiegare il procedimento , quindi motivare la vostra risp:
1) Quale retta ha coefficiente angolare m-3quarti ?
A 3x+4y-2=0
B 3x-2y+3=0
C 6x-8y-3=0
D 6x+8y-7=0

Considerano che ognuna di queste equazioni è nella forma: ax+by+c=0, basterà verificare l’uguaglianza -\frac a b =-\frac 34.

A) il coefficiente angolare è  -\frac 34

B) il coefficiente angolare è \frac 32

C) il coefficiente angolare è \frac 34

B) il coefficiente angolare è -\frac 34

 

Quindi le risposte esatte sono la A e la D.
2)Individuare la retta che passa per P(-2;1):
A 2x+y+2=0
B x+y-5=0
C x+y-1=0
D 3x-y-1=0

Per capire se il punto passa per la retta, basterà sostituire le coordinate del punto alle incognite dell’equazione e verificare dopo la seguente identità:

A) -4+1+2=-1 \neq 0

B) -2+1-5=-6 \neq 0

C) -2+1-1=-2 \neq 0

D) -6-1-1 =-8 \neq 0

Qui credo che sia sbagliata la traccia perchè nessuna retta passa per il punto P.
3) Individuare due rette tra loro parallele (aventi lo stesso coefficiente angolare):
A 2x+y+2=0
B x+y-5=0
C x-y+1=0
D 4x+2y-1=0

Lo svolgimento lo dice la traccia stessa: basterà calcolare i coefficienti angolari:

A) m=-2

B) m=-1

C) m=1

D) m=-2

Quindi le due rette parallele sono A e D.
4) L’equazione della retta passante per A (1;3)e B (-1;1)è:
a x+y-2=0
b x-y-1=0
c x-y+3=0
d x-y+2=0

L’equazione della retta passante per 2 punti è: \frac {y-y_A}{y_B-y_A}=\frac {x-x_A}{x_B-x_A}. Sostituendo otteniamo:

\frac {y-3}{1-3}=\frac {x-1}{-1-1}, da cui:

y-3=x-1 \rightarrow x-y+2=0
5) Quale segmento di estremi A e B ha lunghezza uguale a 5 7 :
A(-2;1)B (1;4)
A(-1;1) B (1;5)
A (-2;1) B (1;5)
A (-1;1) B ( 1;3)

Per calcolare la distanza tra due punti usiamo la formula d=\sqrt {(x_B-x_A)^2 + (y_B-y_A)^2}.

A) d=\sqrt {(1+2)^2 + (4-1)^2}=\sqrt {9+9}=3\sqrt 3.

B) d=\sqrt {(1+1)^2 + (5-1)^2}=\sqrt {4+16}=2\sqrt 5.

C) d=\sqrt {(1+2)^2 + (5-1)^2}=\sqrt {9+16}=5.

D) d=\sqrt {(1+1)^2 + (3-1)^2}=\sqrt {4+4}=2\sqrt 2.

Non è chiara la traccia, ma credo la risposta sia la C.
6) L’equazione della retta passante per A (-1;1) e B ( 1;3)è:
x+y-2=0
x-y-1=0
x-y+3=0
x-y+2=0

L’esercizio è identico all’esercizio 4; sono solo invertiti i punti A e B. Di conseguenza la retta sarà sempre la stessa e la soluzione anche. Risposta D.
7) Le rette di equazioni 2x-4y+1=0 e 2x+y-5=0
a sono tra loro parallele ( coefficiente angolare uguale m*m)
b sono tra loro perpendicolari (m*m-1)
c non so né parallele né perpendicolari
d formano quattro angoli acuti

Analizziamo i coefficienti angolari delle due rette:

m_1=\frac 12

m_2= -2

Quindi le rette sono tra di loro perpendicolare, notando che: m_1*m_2=-1.
8) Individuare l’unica retta che passa per il punto A ( -1;-3):
y=-3x-1
y=-x-3
y=x-3
y=x-2

Come detto in precedenza, verifichiamo l’identità. La risposta esatta è la D.
9) In forma esplicita l’equazione 3x+6y-2=0 diventa:
y=  1mezzox+2
y=1mezzox+1terzo
y=-1mezzox+2
y=1mezzox-1terzo

Svolgiamo tutti i passaggi: 6y=-3x+2 \rightarrow y=-\frac 12 x + \frac 13. Sono sbagliato le risposte, infatti il risultato non è presente nelle quattro.
10) L’equazione della retta passante per A (-1;1) e B (1;3) è:
x+y-2=0
x-y-1=0
x-y+3=0
x-y+2=0

Questo è esercizio è uguale al 6.

 

Ora qua sotto ci sono due es da fare sul quaderno ….
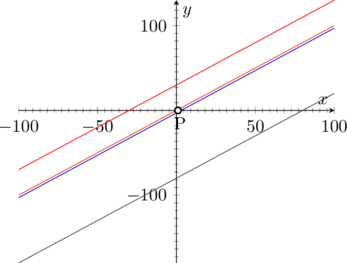
11) Assegnata la retta di equazione y^m-3, rappresentala sul piano cartesiano. Scrivere e disegnare, inoltre, le equazioni di n.3 rette ad essa parallela
di cui una passante per l’origine degli assi.

 

Rendered by QuickLaTeX.com

 

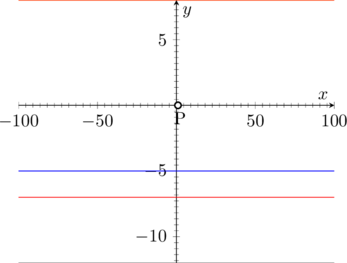
12) Data l’equazione x=-5, rappresentala sul piano cartesiano. Scrivere e disegnare,inoltre, le equazioni di n.3 rette ad essa parallele di cui una passante per l’origine degli assi-

 

Rendered by QuickLaTeX.com

 

(Questa pagina è stata visualizzata da 116 persone)

Lascia un commento