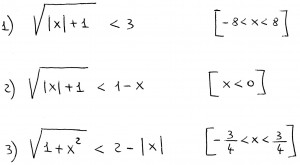Oggetto: Disequazioni irrazionali
Corpo del messaggio:
Distinguiamo due casi:
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ \sqrt { x +1}<3 \end{cases} \quad \quad \begin{cases}x < 0 \\ \sqrt { -x +1}<3 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-646fd999714e752baefc19caa4602256_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ x +1< 9 \end{cases} \quad \quad \begin{cases}x < 0 \\ -x +1< 9 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-f24ba7cef882d15f3e4aab32a691ef58_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ x < 8 \end{cases} \quad \quad \begin{cases}x < 0 \\ -x < 8 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-f30fee2463d2577ac778bae641e65046_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ x < 8 \end{cases} \quad \quad \begin{cases}x < 0 \\ x > - 8 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-4adba74657f355954a665c711c1b9729_l3.png)
Quindi avremo che il primo sistema sarà verificato per:
![]()
e il secondo per
![]()
Unendo le due soluzioni otteniamo:
![]()
Distinguiamo due casi:
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ \sqrt { x +1}<1-x \end{cases} \quad \quad \begin{cases}x < 0 \\ \sqrt { -x +1}<1-x \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-cf20fbd9b193fb69594f85fcb48e1bda_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ 1-x \geq 0 \\ x +1<1-2x+x^2 \end{cases} \quad \quad \begin{cases}x < 0 \\1-x \geq 0 \\ 1 -x < 1-2x+x^2 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-31bd1338f3bde38910657a5f10c9583e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ x \leq 1 \\ x^2-3x >0 \end{cases} \quad \quad \begin{cases}x < 0 \\x \leq 1 \\ x^2-x>0 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-28a329ab1c4a306f9ff06bb5cf7ce8e1_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \geq 0 \\ x \leq 1 \\ x<0 \quad \lor \quad x>3 \end{cases} \quad \quad \begin{cases}x < 0 \\x \leq 1 \\ x<0 \quad \lor \quad x>1 \end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-a4c7100a0e795626dc2af0eaf84a26ad_l3.png)
Quindi avremo che il primo sistema non è mai verificato, mentre il secondo, che darà la soluzione della disequazione iniziale, sarà verificato per
![]()
Essendo ![]() sempre positivo, ci limiteremo a studiare:
sempre positivo, ci limiteremo a studiare:
![Rendered by QuickLaTeX.com \[\begin{cases} 2- \left|x\right| >0 \\ 1+x^2<4+x^2-4 \left|x \right|\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-de98ad3bd2efcfa010365199f9ff2af6_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -2 <x<2\\ 4\left| x \right |<3\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-829e26a2ebb5655b685d62fd74b5471e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -2 <x<2\\ -\frac 34 <x<\frac 34\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-6b8b281649726484b4cc93b329a763a8_l3.png)
Intersecando il tutto otteniamo:
![]()
(Questa pagina è stata visualizzata da 148 persone)