Oggetto: E per domani rispondete  ….

Corpo del messaggio:
data la retta 3x-2y+9=0 verifica se il punto p (-2;5) appartiene a r .Srivere l’ euqazione dellta retta a) passante per P e parallela all’asse x ,b) passante per P e parallela all’asse y, c) passante per P e per l’orgione d) passante per P e perpendicolare a r , e) calcolare la distanza dal putno Q ( 6,-4)dalla retta  r, f) rappresentare sul p.c. le rette di  cui sopra.

 

Risposta dello staff

Innanzitutto vorrei precisare che sarebbe sempre ben gradita un po’ di gentilezza nella richiesta degli esercizi; l’oggetto di questa richiesta è abbastanza fuori luogo, ma sicuramente ci sarà stato un equivoco nello scriverlo, visto che, comunque, riconosciamo ed apprezziamo l’educazione delle persone che frequentano questo sito.

Ma veniamo all’esercizio:

Per verificare l’appartenenza del punto alla retta, basterà sostituire al posto delle incognite nell’equazione le coordinate del punto, ed in seguito verificare l’identità.

Avremo quindi:

Non essendo verificata allora il punto P non appartiene alla retta.

a) La retta avrà equazione:

 

b) La retta avrà equazione

 

c) La retta avrà equazione:

 

d) Affinchè sia perpendicolare ad r dobbiamo calcolare il suo coefficiente angolare:

.

Di conseguenza la retta perpendicolare avrà coefficiente angolare :

Imponiamo il passaggio per P di una generica equazione

Quindi avremo:

.

 

e) Per calcolare la distanza punto retta ci viene incontro la formula nota:

dove a,b e c sono i coefficienti della retta conosciuta e e le coordinate del punto in questione. Avremo:

 

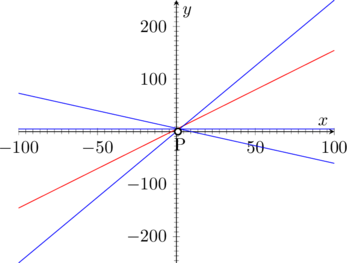
f) (da completare)

 

(Questa pagina è stata visualizzata da 91 persone)