Sharon scrive: Problema di geometria

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Problema di geometria

Corpo del messaggio:
La somma dei cateti di un triangolo rettangolo misura 9,8 centimetri e uno è i 9/40 dell’altro. Calcola perimetro e area del triangolo.

 

Risposta dello staff

Dai dati, ponendo x e y i due cateti, sappiamo che:

\begin{cases} x+y= 9,8 \\ x=\frac {9}{40} y\end{cases}

\begin{cases} \frac {9}{40}y+y= 9,8 \\ x=\frac {9}{40} y\end{cases}

\begin{cases} \frac {49}{40}y= 9,8 \\ x=\frac {9}{40} y\end{cases}

\begin{cases} y= 8 \\ x=\frac {9}{40} y\end{cases}

\begin{cases} y= 8 \\ x=1,8\end{cases}

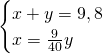
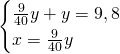
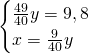
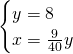
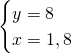
Da qui possiamo calcolare subito l’area:

A=\frac {x \cdot y}{2}=\frac {1,8 \cdot 8}{2} \mbox{ cm}^2=7,2\mbox{ cm}^2

Per calcolare il perimetro ci servirà calcolare l’ipotenusa con il teorema di Pitagora:

i=\sqrt{x^2+y^2}=\sqrt{3,24+64} \mbox{ cm}=\sqrt{67,24}\mbox{ cm}=8,2\mbox{ cm}

(Questa pagina è stata visualizzata da 66 persone)

Lascia un commento