Oggetto: problema triangolo rettangolo.

Corpo del messaggio:
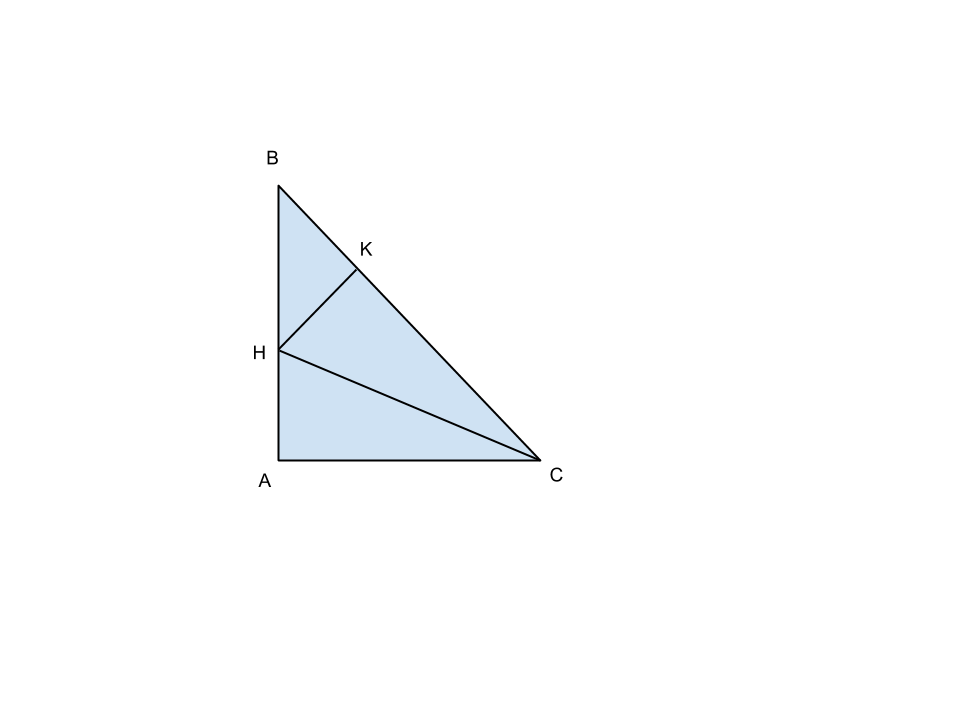
Nel triangolo ABC, rettangolo in A, la bisettrice dell’angolo C incontra il cateto AB nel punto H. Traccia da H la perpendicolare HK all’ipotenusa BC. calcola il perimetro del triangolo BHK, sapendo che AB=12 cm e che si ha BC + AC= 24 cm.

Grazie.

 

Risposta dello staff

Ricaviamo subito i lati del triangolo iniziale. Poniamo , e avremo quindi :

e, per il teorema di Pitagora:

Quindi avremo:

.

Il perimetro del triangolo ABC è quindi:

Sfruttiamo ora il teorema della bisettrice: in ogni triangolo la bisettrice di un angolo interno divide il lato opposto in due segmenti direttamente proporzionali agli altri due lati. Di conseguenza avremo:

Chiamamo

Sostituendo otteniamo:

Ora, notando che i triangoli ABC e BHK sono simili, e che il rapporto tra le due ipotenuse BH e BC è di 1 a 2 (7,5 e 15), avremo che anche il rapporto dei due perimetri è lo stesso e quindi:

(Questa pagina è stata visualizzata da 124 persone)