Giulia scrive: Equazioni parametriche

Oggetto: equazioni parametriche

Corpo del messaggio:

$(k-2)x^2-(2k-1)x+k=0$

Affinchè le soluzioni siano reali e distinte deve accadere che il 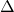$\Delta$ sia strettamente positivo; quindi

$\Delta=(2k-1)^2-4k(k-2)=4k^2-4k+1-4k^2+8k=4k+1$

Basterà quindi porre:

$4k+1>0$

$k>-\frac 14$

ricordando che per $k=2$ , però, l’equazione diventerebbe di primo grado…

Affinchè una soluzione valga 2, basterà sostituire al posto dell’incognita il valore richiesto ed otteniamo:

$4(k-2)-2(2k-1)+k=0$

$4k-8-4k+2+k=0$

$k=6$

Affinchè le due radici siano una l’opposta dell’altra, deve accadere che il coefficiente del termine di primo grado sia nullo, e quindi:

$2k-1=0$

$k=\frac 12$ .

La soluzione è accettabile perchè, con questo valore, il $\Delta$ è cmq positivo.

$\frac {1}{x_1}+\frac {1}{x_2}=\frac {x_1+x_2}{x_1x_2}=-\frac {b}{c}$

Poniamo quindi:

$-\frac {-(2k-1)}{k}=1$

Ponendo $k \neq 0$ , avremo:

$2k-1=k$

$k=1$

(Questa pagina è stata visualizzata da 68 persone)

Matebook