Giulia scrive: Equazioni parametriche 2

Oggetto: equazioni parametriche

Corpo del messaggio:

$kx^2-2(k-1)x+k-2=0$

$\Delta=4(k-1)^2-4k(k-2)=4k^2-8k+4-4k^2+8k=4$

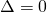Questa equazione quindi non avrà mai due radici coincidenti.

$x_1=-\frac{1}{x_2} \rightarrow x_1 x_2=-1$

Quindi basterà porre:

$\frac ca=\frac {k-2}{k}=-1$

Imponendo che $k \neq 0$ , avremo:

$k-2=-k$

$k=1$

$x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=(-\frac ba)^2-2\frac ca$

Sostituiamo e otteniamo:

$\left(\frac {2(k-1)}{k} \right)^2-2\frac {k-2}{k}=\frac{10}{9}$

$\frac {4k^2-8k+4)}{k^2}-2\frac {k-2}{k}-\frac{10}{9}=0$

Imponendo che $k \neq 0$ , avremo:

$36k^2-72k+36-18k^2+36k-10k^2=0$

$8k^2-36k+36=0$

$2k^2-9k+9=0$

$k_{\frac 12}=\frac {9 \pm \sqrt {81-72}}{4}=\frac {9 \pm 3}{4}$

$k_1=\frac 32$

$k_2=3$

(Questa pagina è stata visualizzata da 51 persone)

Matebook