Giulia scrive: Equazioni parametriche 4

Pubblicato il 14 Maggio 2014 da Lo StaffLascia un commento

Oggetto: equazioni parametriche

Corpo del messaggio:

Risposta dello staff

$x^2-2(a-1)x+a^2-1=0$

Per capire se ammette radici reali, basterà imporre la positività del $\Delta$ .

$\Delta=4(a-1)^2-4(a^2-1)=4a^2-8a+4-4a^2+4=8-8a$

$8-8a \geq 0$

$a \leq 1$

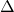Per avere una radice nulla, basterà imporre l’assenza del termine noto, e quindi:

$a^2-1=0$

$a= \pm 1$

Affinchè le radici siano opposte, deve verificarsi che la loro somma faccia 0, e quindi:

$-\frac ba=0$

$2(a-1)=0$

$a=1$

Affinchè le due radici siano antireciproche, dovremo avere:

$x_1=-\frac{1}{x_2} \rightarrow x_1 x_2=-1$

Quindi basterà porre:

$\frac ca=a^2-1=-1$

$a=0$

La somma dei quadrati delle soluzioni sarà:

$x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=(-\frac ba)^2-2\frac ca$

Sostituiamo e otteniamo:

$(2(a-1))^2-2(a^2-1)=16$

$4a^2-8a+4-2a^2+2-16=0$

$2a^2-8a-10=0$

$a^2-4a-5=0$

$(a-5)(a+1)=0$

$a=5 \quad \lor \quad a=-1$

Ma $a=5$ nn è accettabile.

$x_1+x_2-2x_1x_2+40=0$

$2(a-1)-2(a^2-1)+40=0$

$2a-2-2a^2+2+40=0$

$2a^2-2a-40=0$

$a^2-a-20=0$

$(a-5)(a+4)=0$

Ammetterà solo $a=-4$ come soluzione.

(Questa pagina è stata visualizzata da 47 persone)

Lascia un commento Annulla risposta

Devi essere connesso per inviare un commento.