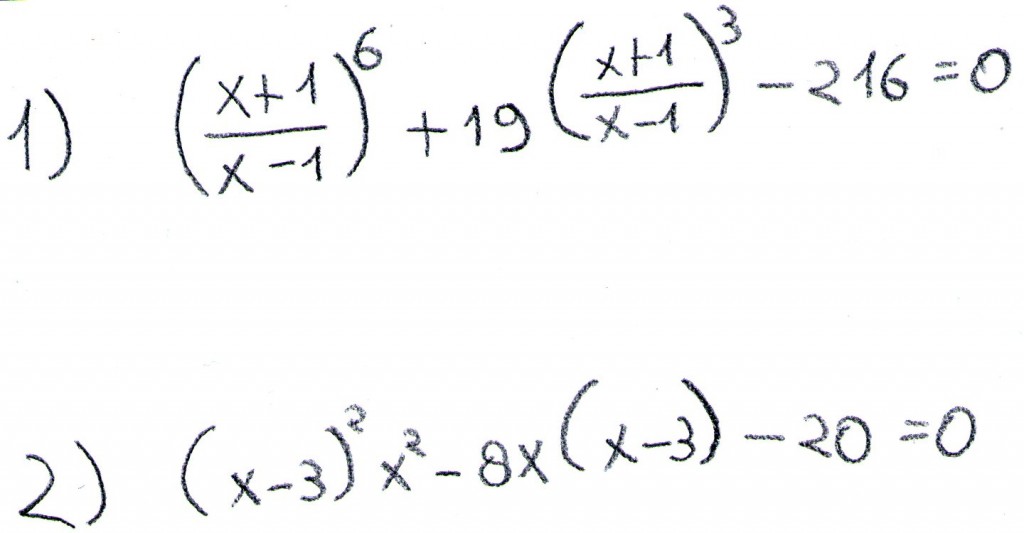Alessandra scrive: equazioni risolubili mediante sostituzioni

Pubblicato il 17 Maggio 2014 da Lo StaffLascia un commento

Oggetto: equazioni risolubili mediante sostituzioni

Corpo del messaggio:

Risposta dello staff

Nella prima equazione poniamo:

$y=\left(\frac {x+1}{x-1}\right)^3$ così da ottenere:

$y^2+19y-216=0$

$y_{frac 12}=\frac {-19 \pm \sqrt {361+864}}{2}=\frac {-19 \pm \sqrt {1225}}{2}=\frac {-19 \pm 35}{2}$

$y_1=-27$

$y_2=8$

Quindi avremo:

$\left(\frac {x+1}{x-1}\right)^3=-27$

$\frac {x+1}{x-1}=-3$

$x+1=-3x+3$

$4x=2$

$x=\frac 12$

oppure:

$\left(\frac {x+1}{x-1}\right)^3=8$

$\frac {x+1}{x-1}=2$

$x+1=2x-2$

$x=3$

Entrambi soluzioni accettabili perchè diverse da 1.

Stesso discorso per il secondo esercizio:

Poniamo $x-3=y$ ed avremo:

$x^2y^2-8xy-20=0$

$(xy-10)(xy+2)=0$

Quindi avremo:

$xy=10 \quad \wedge \quad xy=-2$

da cui:

$x(x-3)=10$

$x^2-3x-10=0$

$(x-5)(x+2)=0$

$x=5 \quad \lor \quad x=-2$

oppure

$x(x-3)=-2$

$x^2-3x+2=0$

$(x-2)(x-1)=0$

$x=1 \quad \lor \quad x=2$

(Questa pagina è stata visualizzata da 101 persone)

Lascia un commento Annulla risposta