Cosimo scrive: Esercizio sui trapezi

Pubblicato il da Lo StaffLascia un commento
-1

Oggetto: N21

Corpo del messaggio:

image (4)

 

Risposta dello staff

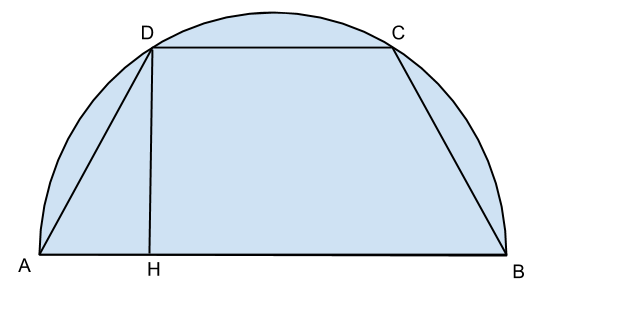
trapezio isoscele semi circonferenza

Determinare la base maggiore AB=2x di un trapezio isoscele ABCD di perimetro di misura 6r circoscritto ad un semicerchio il cui raggio misura r.

Essendo un trapezio circoscritto ad una circonferenza, sappiamo che il lato obliquo risulta essere la metà della base maggiore e quindi:

AD=BC=x

Ora, tracciando l’altezza, che equivale al raggio della semicirconferenza, dal vertice della base minore, otteniamo il triangolo equilatero ADH, e con il teorema di Pitagora ricaviamo AH:

AH=\sqrt{x^2-r^2}

Ora abbiamo tutto, poichè la base minore sarà:

CD=AB-2AH=2x-2\sqrt{x^2-r^2}

Calcoliamo il perimetro e otteniamo:

2x+x+2x-2\sqrt{x^2-r^2}+x=6r

6x-2\sqrt{x^2-r^2}=6r

3x-3r=\sqrt{x^2-r^2}

9x^2-18rx+9r^2=x^2-r^2

8x^2-18rx+10r^2=0

4x^2-9rx+5r^2=0

x_{\frac 12}=\frac {9r \pm \sqrt{81-80}r}{8}=\frac {9r \pm r}{8}

x_1=r

x_2=\frac 54r

Di conseguenza avremo:

AB=2r oppure AB=\frac 52 r

Nella prima soluzione il lato coinciderebbe con il diametro della semicirconferenza e non avremmo più un trapezio isoscele ma un rettangolo.

 

 

(Questa pagina è stata visualizzata da 150 persone)

Lascia un commento