Davide scrive: Equazione parametrica

Pubblicato il da Lo Staff2 commenti
0

Oggetto: equazione parametrica

Corpo del messaggio:
(4-k^2)x^2+2kx+1-k^2=0

Risposta dello staff

 

Calcoliamo subito il \Delta

\Delta=4k^2-4(1-k^2)(4-k^2)=4k^2-16+4k^2+16k^2-4k^4=-4k^4+24k^2-16=-4(k^2-6k+4)

Studiamo la positività del \Delta:

-4(k^2-6k+4)>0

k^2-6k+4<0

k_{\frac 12}=\frac {6 \pm \sqrt {36-16}}{2}=\frac {6 \pm \sqrt {20}}{2}=3 \pm \sqrt 5

Quindi:

  • se 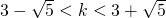3-\sqrt 5<k< 3+\sqrt 5 avremo due soluzioni distinte
  • se 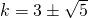k=3 \pm\sqrt 5 avremo due soluzioni coincidenti: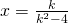 x=\frac {k}{k^2-4}
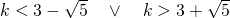  • k<3-\sqrt 5 \quad \lor \quad k>3+\sqrt 5 l’equazione non ammetterà soluzione.

 

 

(Questa pagina è stata visualizzata da 125 persone)

2 pensieri riguardo “Davide scrive: Equazione parametrica”

Lascia un commento