Clara scrive: Studio di una funzione

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Studio di una funzione

Corpo del messaggio:

y=log \frac {x-2}{2}

 

Risposta dello staff

 

  • Insieme di definizione

\frac {x-2}{2} >0

x >2

    \[D= ]2;+\infty [\]

  • Simmetrie e periodicità

-f(x)=-log\frac {x-2}{2}

f(-x)=log\frac {-x-2}{2}

Questa funzione non avrà simmetrie.

  • Intersezioni con gli assi

\begin{cases} y=0 \\ log \frac {x-2}{2}=0 \end{cases}

\begin{cases} y=0 \\ \frac {x-2}{2}=1 \end{cases}

\begin{cases} y=0 \\ x=4 \end{cases}

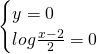
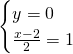
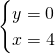
La funzione avrà una intersezione con gli assi:

\left (4;0 \right)

  • Segno della funzione

Studiamo la positività di f(x):

log \frac {x-2}{2} \geq0

\frac {x-2} {2} \geq 1

x-2 \geq 2

x \geq 4

f(x) <0 \quad \mbox{ per } \quad 2<x<4

f(x)=0 \quad \mbox{ per } \quad x=4

f(x) >0 \quad \mbox{ per } \quad x>4

  • condizione agli estremi

    \[\lim_{ x \rightarrow + \infty} f(x)= +\infty\]

    \[\lim_{ x \rightarrow 2^+} f(x)= -\infty\]

  • Asintoti

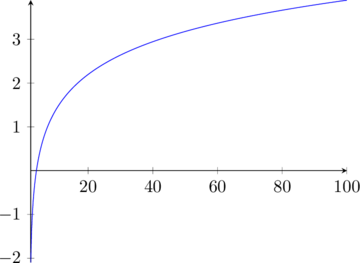
La funzione avrà asintoto verticale in x=2.

  • Studio della derivata prima

y'=\frac {2}{x-2}

y' \geq 0

\frac{2}{x-2} \geq0

Visto che questa disequazione è verificata per ogni valore dell’incognita nel dominio, la funzione sarà sempre crescente. Non avrà massimi e minimi relativi.

  • Studio della derivata seconda

y''=\frac {-2}{(x-2)^2}

y''\geq 0

\frac {-2}{(x-2)^2} \geq0

Visto che questa disequazione non è mai verificata per i valori dell’incognita nel dominio, la funzione avrà sempre concavità rivolta verso il basso. Non avrà punti di flesso.

 

Rendered by QuickLaTeX.com

(Questa pagina è stata visualizzata da 77 persone)

Lascia un commento