Anna scrive: Risoluzione di una funzione

Pubblicato il da EdoLascia un commento
0

Studiare la funzione x +arcsen(1-x). Verificare inoltre che la funzione non è deriva bile agli estremi del dominio e trovare l’equazione dell’approssimante lineare nel punto di flesso

Studiamo la funzione:

    \[f(x)=x+arcsen(1-x)\]

Il dominio sarà dato dal sistema:

\begin{cases} 1-x \geq -1 \\ 1-x \leq 1\end{cases}

\begin{cases} x \leq 2 \\ x \geq 0\end{cases}

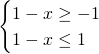
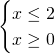
Avremo quindi:

D \, : \, \, [0;2]

Ci accorgiamo senza grossi calcoli che la funzione sarà sempre positiva, in quanto:

f(0)=arcsen(1)=\frac 12 \pi

f(1)=1

f(2)=2-\frac 12 \pi>0.

Ovviamente, per ora non ne abbiamo la certezza, ma verificheremo in seguito.

Calcoliamo la derivata prima, visto che i limiti agli estremi non sarà necessario studiarli:

f'(x)=1+\frac {-1}{\sqrt{1-(1-x)^2}}=1-\frac {1}{\sqrt{2x-x^2}}

Notiamo che, come in quasi tutte le funzioni in cui è presente l’arcoseno, se calcolassimo il limite della derivata negli estremi, non riusciremmo a calcolarne il valore. La funzione è continua ma non derivabile negli estremi.

Inoltre, notiamo che la derivata è sempre negativa, tranne che per x=1 dove la derivata è nulla.

Quindi la funzione è sempre decrescente, ma ha in 1 un punto particolare che analizziamo studiando la derivata seconda.

Calcoliamo la derivata seconda e otteniamo:

f''(x)=\frac {2-2x}{\sqrt{(2x-x^2)^3}}

dove il denominatore è sempre positivo e quindi la concavità è data solo dalla positività del numeratore.

Quindi la funzione avrà concavità verso l’alto in [0;1] e verso il basso in [1;2].

Come ci si aspettava, x=1 è punto di flesso.

Troviamo l’approssimante lineare nel punto di flesso con il polinomio di Taylor:

y=f(1)+f'(1)(x-1)+o(x-1)

y=1

(Questa pagina è stata visualizzata da 71 persone)

Lascia un commento