Assunta scrive: esercizio 2

Pubblicato il da EdoLascia un commento
0

Nell’equazione kx^2-y^2=4 si determini il valore di k in modo che il grafico della curva passi per il punto A(2;2\sqrt 3). Si determininino le coordinate dei vertici e dei fuochi della curva e le equazioni degli asintoti. Si trovi quindi l’equazione della circonferenza di centro l’origine e passante per i punti di intersezione tra l’iperbole precedentemente determinata e l’iperbole di equazione xy=13\sqrt 2.

Risposta dello staff

 

Ricaviamo k:

4k-12=4

k=4

L’equazione dell’iperbole diventa quindi:

4x^2-y^2=4

o meglio

x^2-\frac {y^2}{4}=1

I vertici saranno:

V(\pm 1;0)

I fuochi saranno:

F(\pm \sqrt 5,0)

Gli asintoti saranno:

y= \pm 2x

Una generica equazione di centro O sarà del tipo:

x^2+y^2=r^2.

Per ricavare r troviamo il punto di intersezione delle iperboli:

\begin{cases} 4x^2-y^2=4 \\ xy=12\sqrt 2 \end{cases}

\begin{cases} 4x^2-y^2=4 \\ x= \frac {12\sqrt 2}{y} \end{cases}

\begin{cases} \frac {1152}{y^2}-y^2=4 \\ x= \frac {12\sqrt 2}{y} \end{cases}

\begin{cases}1152-y^4-4y^2=0 \\ x= \frac {12\sqrt 2}{y} \end{cases}

\begin{cases} y^4+4y^2-1152=0 \\ x= \frac {12\sqrt 2}{y} \end{cases}

\begin{cases} (y^2+36)(y^2-32)=0 \\ x= \frac {12\sqrt 2}{y} \end{cases}

\begin{cases} y=\pm 4\sqrt 2 \\ x= \frac {12\sqrt 2}{y} \end{cases}

\begin{cases} y=\pm 4\sqrt 2 \\ x= \pm 3 \end{cases}

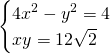
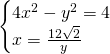
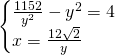
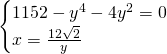
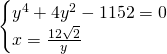
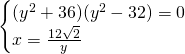
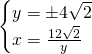
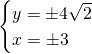
I due punti saranno:

(3;4\sqrt2) e (-3;-4\sqrt2)

Andando a sostituire nell’equazione della circonferenza troviamo r:

9+32=r^2

r^2=41

da cui l’equazione:

x^2+y^2=41.

(Questa pagina è stata visualizzata da 67 persone)

Lascia un commento