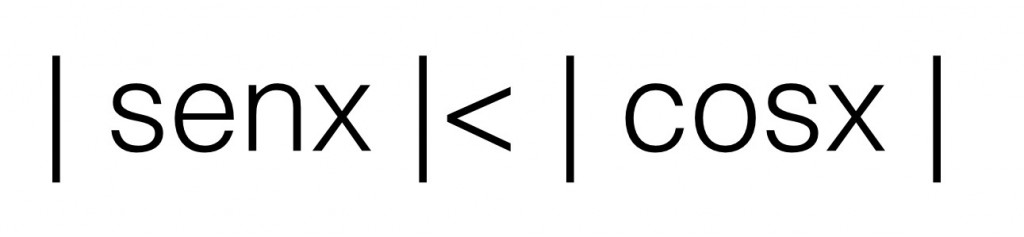Oggetto: DISEQUAZIONE TRIGONOMETRICA
Corpo del messaggio:
Risolvere la seguente disequazione
Risposta dello staff
![]()
![]()
Andiamo quindi ad analizzare le casistiche e poi ad unire le soluzioni:
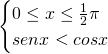

La soluzione del primo sistema è: ![]()
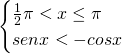
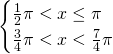
La soluzione del secondo sistema è: ![]()
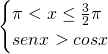
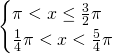
La soluzione del primo sistema è: ![]()
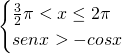
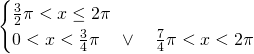
La soluzione del primo sistema è: ![]()
Unendo tutte le soluzioni otteniamo:
![]() .
.
(Questa pagina è stata visualizzata da 70 persone)