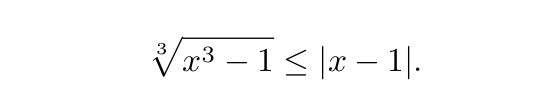Mario scrive: Disequazione

Oggetto: Disequazione

Corpo del messaggio:
Svolgere la seguente disequazione:

$\sqrt[3]{x^3-1} \leq \left|x-1 \right|$

$\begin{cases} x \geq 1 \\ \sqrt[3]{x^3-1} \leq x-1 \end{cases}\quad \begin{cases} x < 1 \\ \sqrt[3]{x^3-1} \leq -(x-1) \end{cases}$

$\begin{cases} x \geq 1 \\x^3-1 \leq x^3-3x^2+3x-1 \end{cases}\quad \begin{cases} x < 1 \\ x^3-1 \leq -x^3+3x^2-3x+1 \end{cases}$

$\begin{cases} x \geq 1 \\ 3x^2-3x \leq 0 \end{cases}\quad \begin{cases} x < 1 \\ (x-1)(x^2+x+1)+(x-1)^3 \leq 0 \end{cases}$

$\begin{cases} x \geq 1 \\ x(x-1) \leq 0 \end{cases} \quad \begin{cases} x < 1 \\ (x-1)(x^2+x+1+x^2-2x+1) \leq 0 \end{cases}$

$\begin{cases} x \geq 1 \\ 0 \leq x \leq 1 \end{cases} \quad \begin{cases} x < 1 \\ (x-1)(2x^2-x+2) \leq 0 \end{cases}$

Il secondo fattore nel secondo sistema è sempre positivo, quindi:

$\begin{cases} x \geq 1 \\ 0 \leq x \leq 1 \end{cases} \quad \begin{cases} x < 1 \\ x \leq 1 \end{cases}$

Il primo sistema ammetterà come soluzione $x=1$ , mentre il secondo $x \leq 1$ .

Unendo le soluzioni avremo:

$x \leq -1$

(Questa pagina è stata visualizzata da 49 persone)

Matebook