Alessandra scrive: Numeri Complessi

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Numeri Complessi

Corpo del messaggio:
ex 1 Risolvi l’equazione (z-i-1)³=8i e scrivi le soluzioni in forma algebrica.

 

Risposta dello staff

t=z-i-1

t^3=8i

t=x+iy

(x+iy)^3=8i

x^3+i^3y^3+3x^2iy+3xi^2y^2=8i

x^3-iy^3+3x^2iy-3xy^2=8i

Dividendo parte reale e parte immaginaria otteniamo:

(x^3-3xy^2)+i(3x^2y-y^3)=i

\begin{cases} x^3-3xy^2=0 \\ 3x^2y-y^3=8 \end{cases}

\begin{cases} x(x^2-3y^2)=0 \\ 3x^2y-y^3=8 \end{cases}

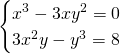
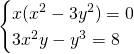
Per la legge dell’annullamento del prodotto avremo che una soluzione è data da x=0, che sostituendo nel secondo sistema darà y=-2. Troviamo le alte soluzioni:

\begin{cases} x^2-3y^2=0 \\ 3x^2y-y^3=8 \end{cases}

\begin{cases} x^2=3y^2 \\ 3x^2y-y^3=8 \end{cases}

\begin{cases} x^2=3y^2 \\ 9y^3-y^3=8 \end{cases}

\begin{cases} x^2=3y^2 \\ 8y^3=8 \end{cases}

\begin{cases} x^2=3y^2 \\ y^3=1 \end{cases}

\begin{cases} x^2=3y^2 \\ y=1 \end{cases}

\begin{cases} x^2=3 \\ y=1 \end{cases}

\begin{cases} x=\pm \sqrt 3 \\ y=1 \end{cases}

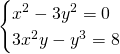
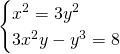
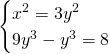
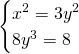
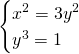
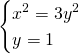
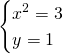
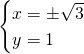
Quindi, le tre soluzioni sono:

t_1= -2i

t_2=\sqrt 3 +i

t_3=-\sqrt 3 +i

Da queste, ricaviamo z, sapendo che z=t+1+i

z_1= 1-i

z_2=1+\sqrt 3 +2i

z_3=1-\sqrt 3 +2i

 

(Questa pagina è stata visualizzata da 84 persone)

Lascia un commento