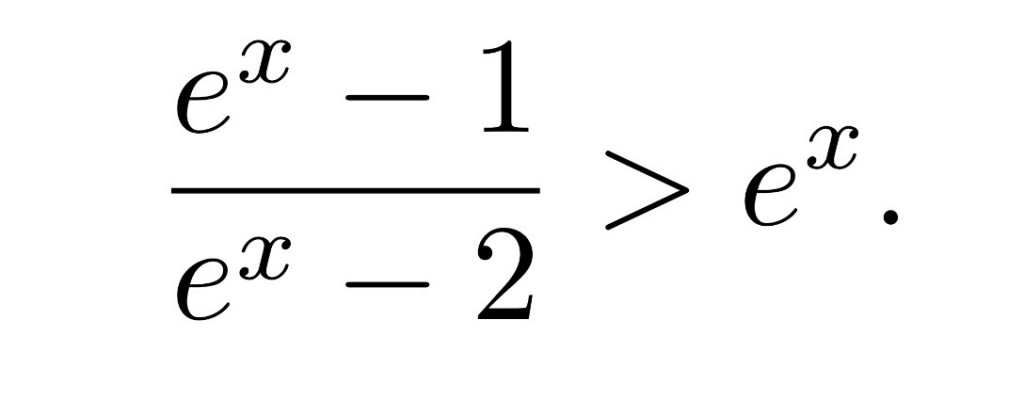Luca scrive: Disequazione

Oggetto: Disequazione

Corpo del messaggio:
Svolgere la seguente disequazione:

$\frac {e^x-1}{e^x-2} > e^x$

$\frac {e^x-1-e^{2x}+2e^x}{e^x-2} >0$

$\frac {-1-e^{2x}+3e^x}{e^x-2} >0$

$\frac {e^{2x}-3e^x+1}{e^x-2} <0$

Analizziamo separatamente numeratore e denominatore:

$e^x_{\frac 12}= \frac {3 \pm \sqrt {9-4}}{2}=\frac {3 \pm \sqrt {5}}{2}$

$e^x < \frac {3 - \sqrt {5}}{2} \quad \lor \quad e^x > \frac {3 +\sqrt {5}}{2}$

$x < log(\frac {3 - \sqrt {5}}{2}) \quad \lor \quad x >log( \frac {3 +\sqrt {5}}{2})$

Unendo le soluzioni, otteniamo la soluzione della disequazione iniziale:

$x<log(\frac {3 - \sqrt {5}}{2}) \quad \lor \quad 2<x<log(\frac {3 + \sqrt {5}}{2})$

(Questa pagina è stata visualizzata da 62 persone)

Matebook