Matteo scrive: problema da risolvere con le equazioni

Oggetto: problema darisolvere con le equazioni

Corpo del messaggio:
in un triangolo ABC la base AB è i 6/5 del lato obliquo. l’altezza relativa al lato obliquo AK è uguale all’altezza del triangolo + 4 cm. individuare il lato obliquo e il perimetro del triangolo.
grazie

Risposta dello staff

Suppongo che il triangolo sia isoscele…

Dai dati abbiamo che:

$AB=\frac 65 BC$

$AK=CH+4$

Sapendo che l’area è uguale, e, ponendo come due incognite la base e l’altezza relativa, avremo:

$AB=x$

$CH=y$

$BC=\frac 56x$

$AK=y+4$

Risolviamo quindi il sistema:

$\begin{cases} xy=\frac 56x(y+4) \\ \left(\frac x2 \right)^2 + y^2= \left(\frac 56x\right)^2 \end{cases}$

$\begin{cases} 6xy=5xy+20x \\ \frac {x^2}{4} + y^2= \frac{25x^2}{36} \end{cases}$

$\begin{cases} xy-20x=0 \\ 9x^2 + 36y^2= 25x^2 \end{cases}$

$\begin{cases} x(y-20)=0 \\ 36y^2= 16x^2 \end{cases}$

$\begin{cases} y=20 \\ 6y= 4x \end{cases}$

$\begin{cases} y=20 \\ x=30 \end{cases}$

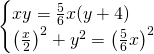
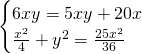
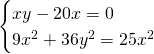
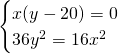
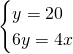
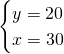
da cui:

$AB=30 \mbox{ cm}$

$CH=20 \mbox{ cm}$

$BC=25 \mbox{ cm}$

$AK=24 \mbox{ cm}$

$2p=(30+25+25) \mbox{ cm}=80\mbox{ cm}$

(Questa pagina è stata visualizzata da 84 persone)

Matebook

La matematica spiegata passo passo

Matteo scrive: problema da risolvere con le equazioni

Risposta dello staff

Lascia un commento Annulla risposta