Graziano scrive: radicali doppi disequazione

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: radicali doppi disequazione

Corpo del messaggio:
è un po sfuocato.Cmq i numeri sono:radice quadra di 4 elevato alla x per 2 elevato alla x più radice quadra di 8 elevato alla x meno 1 (la seconda radice è “sotto” la prima) minore o uguale a radice quadra di 2 elevato alla 3x più 1 meno 1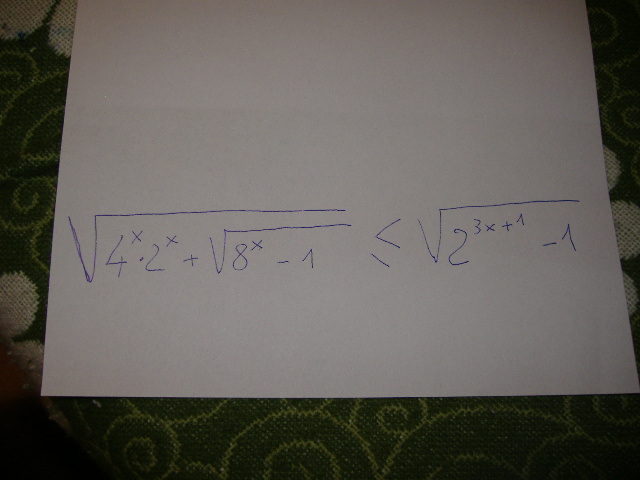rad-doppi

 

 

Risposta dello staff

\sqrt{4^x \cdot 2^x + \sqrt{8^x-1}} \leq \sqrt{2^{3x+1}-1}

\sqrt{2^{2x} \cdot 2^x + \sqrt{2^{3x}-1}} \leq \sqrt{2^{3x+1}-1}

\sqrt{2^{3x} + \sqrt{2^{3x}-1}} \leq \sqrt{2^{3x+1}-1}

Eleviamo al quadrato ed otteniamo:

\begin{cases} 2^{3x} + \sqrt{2^{3x}-1}} \leq 2^{3x+1}-1 \\ 2^{3x}-1 \geq 0 \\ 2^{3x+1}-1 \geq 0\end{cases}

\begin{cases} \sqrt{2^{3x}-1}} \leq 2^{3x+1}-1-2^{3x} \\ 3x \geq 0 \\ 3x+1 \geq 0\end{cases}

\begin{cases} \sqrt{2^{3x}-1} \leq 2^{3x}-1 \\ x \geq 0 \\ x \geq -\frac 13 \end{cases}

eleviamo nuovamente al quadrato, eliminando la terza condizione poichè superflua:

\begin{cases} 2^{3x}-1 \leq 2^{6x}-2 \cdot 2^{3x}+1 \\ x \geq 0 \\ \end{cases}

\begin{cases} 2^{6x}-3 \cdot 2^{3x}+2 \geq 0 \\ x \geq 0 \\ \end{cases}

Ponendo 2^{3x}=t

t^2-3t+2 \geq0

(t-2)(t-1) \geq 0

t \leq 1 \quad \lor \quad t \geq 2

2^{3x}\leq 1 \quad \lor \quad 2^{3x] \geq 2

3x\leq 0 \quad \lor \quad 3x \geq 1

x\leq 0 \quad \lor \quad x \geq \frac 13

Da cui, la soluzione è:

x \geq \frac 13

(Questa pagina è stata visualizzata da 77 persone)

Lascia un commento