Oggetto: Svolgimento problema di geometria piana risolubile con equazioni di primo grado

Corpo del messaggio:
Se è possibile farmi 4 problemi…

Risposta dello staff

1) Determina l’ampiezza di 3 angoli di un triangolo isoscele sapendo che l’angolo vertice supera di 15° ciascuno degli angoli alla base. [55,55,70]

Essendo un triangolo isoscele, sappiamo che i due angoli alla base sono uguali e quindi risolviamo il sistema:

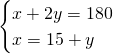
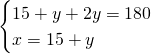
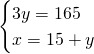
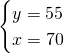
2)Determina l’ampiezza dei 3 angoli di un triangolo isoscele sapendo che ciascuno degli angoli alla base supera di 12° i 3/7 dell’angolo al vertice. [48,48,84]

Essendo un triangolo isoscele, sappiamo che i due angoli alla base sono uguali e quindi risolviamo il sistema:

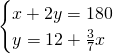
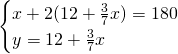
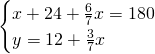
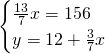
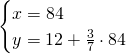
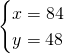
3)Determina la lunghezza di 2 segmenti sapendo che il primo supera il secondo di 26 cm ed è 3/4 della loro somma [39cm,13cm]

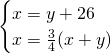
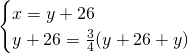
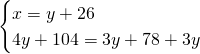
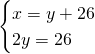
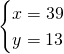
4)Quanto sono lunghi 2 segmenti se la loro somma è 86cm e i 3/7 del primo hanno la stessa lunghezza dei 4/5 del secondo? [56cm,30cm]

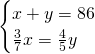
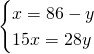
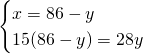
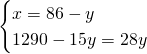
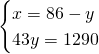
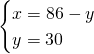
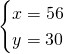
Mi servirebbero per domani se è possibile farli tutti e 4 …

(Questa pagina è stata visualizzata da 63 persone)