Michelangelo scrive: trapezio

Pubblicato il 3 Dicembre 2014 da Lo StaffLascia un commento

Oggetto: ho la necessità di vedere la spiegazione

Corpo del messaggio:
In un trapezio la somma delle basi è 450 cm, l’altezza misura 160 cm e i 5/7 della base magg. superano di 190 cm i 3/5 della base minore. Sapendo che il rapporto delle proiezioni dei lati obliqui sulla base magg. è 16/9, calcola il perimetro del trapezio.

Risposta dello staff

dai dati abbiamo che:

$\begin{cases} B+b=450\mbox{ cm} \\ \frac 57 B =190\mbox{ cm}+ \frac 35 b\end{cases}$

$\begin{cases} b=450\mbox{ cm}-B \\ \frac 57 B =190\mbox{ cm}+ \frac 35(450\mbox{ cm}-B)\end{cases}$

$\begin{cases} b=450\mbox{ cm}-B \\ \frac 57 B =190\mbox{ cm}+ 270\mbox{ cm} -\frac 35B \end{cases}$

$\begin{cases} b=450\mbox{ cm}-B \\ \frac {25+21}{35} B =460\mbox{ cm} \end{cases}$

$\begin{cases} b=450\mbox{ cm}-B \\ \frac {46}{35} B =460\mbox{ cm} \end{cases}$

$\begin{cases} b=450 \mbox{ cm}-B \\ B =350\mbox{ cm} \end{cases}$

$\begin{cases} b=100 \mbox{ cm} \\ B =350 \mbox{ cm} \end{cases}$

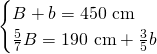
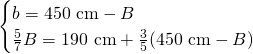
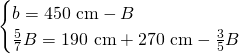
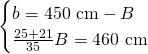
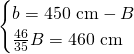
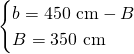
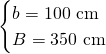
Ora sappiamo anche che:

$\begin{cases} BH+AK=250\mbox{ cm} \\ BH=\frac{16}{9}AK \end{cases}$

$\begin{cases} \frac{16}{9}AK+AK=250\mbox{ cm} \\ BH=\frac{16}{9}AK \end{cases}$

$\begin{cases} \frac{25}{9}AK=250 \mbox{ cm} \\ BH=\frac{16}{9}AK \end{cases}$

$\begin{cases}AK=90\mbox{ cm} \\ BH=\frac{16}{9}AK \end{cases}$

$\begin{cases}AK=90\mbox{ cm} \\ BH=160\mbox{ cm} \end{cases}$

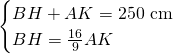
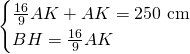
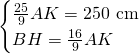
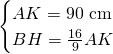
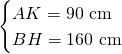
Conoscendo l’altezza calcoliamo i 2 lati obliqui con pitagora:

$AD=\sqrt{AK^2+DK^2}=\sqrt{8100+25600}\mbox{ cm}=\sqrt{33700}\mbox{ cm}=10\sqrt{337}\mbox{ cm}$

$BC=\sqrt{CH^2+BH^2}=\sqrt{25600+25600}\mbox{ cm}=160\sqrt{2}\mbox{ cm}$

Il perimetro sarà quindi:

$2p=(450+10 \sqrt{337}+160\sqrt{2}) \mbox{ cm}=10(45+\sqrt{337}+16\sqrt{2}) \mbox{ cm}$

(Questa pagina è stata visualizzata da 99 persone)

Lascia un commento Annulla risposta