Lucrezia scrive: procedimento+grafico della seguente funzione 1

Pubblicato il da Edo1 commento
0

y=\frac{\left(x-1\right)^3}{x^2-4}

Risposta dello staff

Calcoliamo il dominio:

x^2-4 \neq 0 \iff x \neq \pm 2

Quindi:

D= \mathbb{R} - \{ \pm2 \}

Calcoliamo la positività:

f(x) >0

\frac{\left(x-1\right)^3}{x^2-4}>0

Studiamo separatamente numeratore e denominatore:

x-1 >0 \iff x>1

x^2-4 >0 \iff x<-2 \quad \lor \quad x>2

Quindi avremo che:

f(x) >0 \iff -2<x<1 \quad \lor \quad x>2

f(x)=0 \iff x=1

f(x) <0 \iff x<-2 \quad \lor \quad 1<x<2

Calcoliamo i limiti negli estremi del dominio:

    \[\lim_{x \to \pm \infty} f(x)= \pm \infty\]

    \[\lim_{x \to -2^-} f(x)= - \infty\]

    \[\lim_{x \to -2^+} f(x)= + \infty\]

    \[\lim_{x \to 2^-} f(x)= - \infty\]

    \[\lim_{x \to 2^+} f(x)= + infty\]

Calcoliamo la derivata prima:

f'(x)=\frac{3(x-1)^2(x^2-4)-(x-1)^3(2x)}{(x^2-4)^2}

f'(x)=\frac{3(x^2-2x+1)(x^2-4)-(x^3-3x^2+3x-1)(2x)}{(x^2-4)^2}

f'(x)=\frac{3x^4-6x^3-9x^2+24x-12-2x^4+6x^3-6x^2+2x}{(x^2-4)^2}

f'(x)=\frac{x^4-15x^2+26x-12}{(x^2-4)^2}

f'(x)=\frac{(x-1)(x^3+x^2-14x+12}{(x^2-4)^2}

f'(x)=\frac{(x-1)^2(x^2+2x-12}{(x^2-4)^2}

Studiamo la positività della derivata prima:

N_1 >0 \iff x \neq 1

N_2 >0 \iff x^2+2x-12 >0 \iff x< -1 - \sqrt{13} \quad \lor \quad x>-1 + \sqrt{13}

D>0 \iff x \neq \pm 2

f'(x)>0 \iff x< -1 - \sqrt{13} \quad \lor \quad x>-1 + \sqrt{13}

f(x)=0 \iff x= -1 - \sqrt{13} \quad \lor \quad x=-1 + \sqrt{13} \quad \lor \quad x=1

f'(x)<0 \iff -1 - \sqrt{13}<x<-2 \quad \lor \quad -2<x<1\quad \lor \quad 1<x<2 \quad \lor \quad 2< x<-1 + \sqrt{13}

Non studiamo la derivata seconda per non appesantire un po’ troppo lo studio…

 

Rendered by QuickLaTeX.com

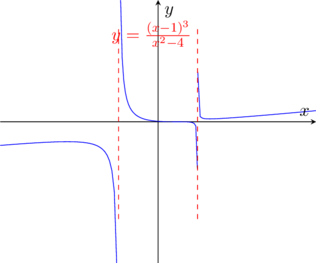
(Questa pagina è stata visualizzata da 78 persone)

Un pensiero riguardo “Lucrezia scrive: procedimento+grafico della seguente funzione 1”

  1. Pingback: Lucrezia scrive: procedimento+grafico delle seguenti funzioni | Matebook

Lascia un commento