Oggetto:

Corpo del messaggio:
un triangolo rettangolo, un rombo e un trapezio sono equivalenti. la somma dei cateti del triangolo misura 84 cm e la loro differenza e 12 cm, il rombo ha una diagonale congruente ai 3\2 del cateto maggiore del triangolo e il trapezio ha l’ altezza congruente all’ altra diagonale del rombo. calcola le misure delle basi del trapezio sapendo che la maggiore  e il triplo della minore.

Risposta dello staff

Essendo equivalenti, vuol dire che i 3 poligoni hanno la stessa area.

Di conseguenza, ricaviamo subito l’area sapendo i cateti del triangolo rettangolo:

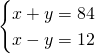
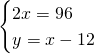
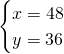
Ora, calcoliamo l’area che è uguale per tutti:

Ora ricaviamo la diagonale del rombo:

sapendo che l’area del rombo è il semiprodotto delle diagonali, ricaviamo la seconda diagonale:

Dalla traccia sappiamo che l’altezza del trapezio è:

.

Sapendo l’area del trapezio ricaviamo la somma delle basi:

Svolgiamo il sistema con l’altra condizione dataci e troviamo le misure:

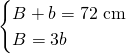
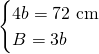
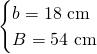
(Questa pagina è stata visualizzata da 84 persone)