Oggetto: Aiuto con studio di funzione a tratti
Corpo del messaggio:
Ciao! Mi aiutereste a risolvere questo studio di funzione definita a tratti? Sono bloccata in un punto e avrei bisogno di sciogliere alcuni dubbi.
La funzione in questione è f(t) { log(t+1) + 2 t>0 e t^2 + 3 t<= 0
Ho trovato un punto angoloso e due punti esclusi ma non sono sicura. Non sono riuscita a fare lo studio del segno delle due funzioni secondarie, ne le intersezioni con gli assi. Non sono sicura dei passaggi che ho già fatto.
Potrei mostrarmi i passaggi così posso capire come svolgere questa tipologia di esercizio? Grazie…
Risposta dello staff
Sia
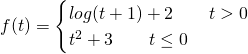
il dominio è ovviamente tutto ![]() , poiche l’unica condizione sarebbe:
, poiche l’unica condizione sarebbe:
![]() ma la funzione assume valori solo per valori di t positivi.
ma la funzione assume valori solo per valori di t positivi.
Studiamo la positività della funzione:
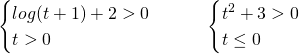
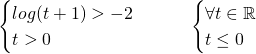
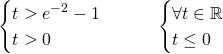
Essendo verificate le condizioni, nel primo sistema ![]() e nel secondo
e nel secondo ![]() , la funzione è positiva per ogni t appartenente al dominio.
, la funzione è positiva per ogni t appartenente al dominio.
Essendo sempre strettamente positiva, ![]() non si verificherà mai.
non si verificherà mai.
Invece per ![]() , come da traccia,
, come da traccia, ![]()
Studiamo i limiti:
![]()
Studiamo la derivata prima:
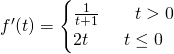
Quindi la funzione è derivabile in ogni punto tranne per ![]()
![]()
![]()
(Questa pagina è stata visualizzata da 101 persone)