Giuseppe scrive: Esercizi di algebra

Pubblicato il da Lo StaffLascia un commento
-1

Oggetto: Trigoniometria e numeri complessi

Corpo del messaggio:
Ciao, le foto degli esercizi che vi sto inviando sono esercizi che non mi riescono quindi vorrei capire con il vostro aiuto come svolgerli, aspetto una risposta in merito gli esercizi. Grazie

CAM01243

 

Risposta dello staff

z_1=2\sqrt 2 \left(cos\frac{11}{6} \pi + i sen \frac{11}{6}\pi\right)

z_2=cos\frac{\pi}{4} + i sen \frac{\pi}{4}

Sfruttiamo la formula:

z_1=r(cos\alpha+isen\alpha)

z_2=r(cos\beta+isen\beta)

\frac{z_1}{z_2}=\frac rs \left[cos(\alpha-\beta)+isen(\alpha-\beta)\right]

avremo quindi:

\frac{z_1}{z_2}=2\sqrt 2 \left[cos(\frac{11}{6} \pi-\frac{\pi}{4})+isen(\frac{11}{6} \pi-\frac{\pi}{4})\right]

da cui:

cos(\frac{11}{6} \pi-\frac{\pi}{4})=cos(\frac{11}{6} \pi)cos(\frac{\pi}{4})+sen(\frac{11}{6} \pi)sen(\frac{\pi}{4})=\frac{\sqrt 3}{2}\frac{\sqrt 2}{2}-\frac 12 \frac{\sqrt 2}{2}=\frac{\sqrt 2}{4}(\sqrt 3-1)

sen(\frac{11}{6} \pi-\frac{\pi}{4})=sen(\frac{11}{6} \pi)cos(\frac{\pi}{4})-cos(\frac{11}{6} \pi)sen(\frac{\pi}{4})=-\frac{1}{2}\frac{\sqrt 2}{2}-\frac {\sqrt3}{2} \frac{\sqrt 2}{2}=-\frac{\sqrt 2}{4}(1+\sqrt 3)

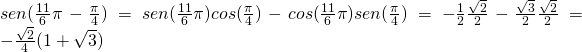
sostituendo il tutto avremo:

\frac{z_1}{z_2}=2\sqrt 2 \left[\frac{\sqrt 2}{4}(\sqrt 3-1) -i\frac{\sqrt 2}{4}(1+\sqrt 3)=\sqrt 3-1-i(1+\sqrt 3)

(Questa pagina è stata visualizzata da 42 persone)

Lascia un commento