Fabio scrive: determina il dominio (potete anche spiegare)?

Oggetto: determina il dominio (potete anche spiegare)?

Corpo del messaggio:

Il dominio di questa funzione va calcolato sapendo che l’argomento dell’arcoseno è compreso tra -1 e 1, quindi:

$-1 \leq \frac{2}{x+2} \leq 1$

$\begin{cases} \frac{2}{x+2} \geq -1\\ \frac{2}{x+2} \leq 1\end{cases}$

$\begin{cases} \frac{2}{x+2} +1\geq 0\\ \frac{2}{x+2}-1 \leq 0 \end{cases}$

$\begin{cases} \frac{2+x+2}{x+2} \geq 0\\ \frac{2-x-2}{x+2} \leq 0 \end{cases}$

$\begin{cases} \frac{x+4}{x+2} \geq 0\\ \frac{x}{x+2} \geq 0 \end{cases}$

$\begin{cases} x \leq -4 \quad \lor \quad x>-2 \\ x <-2 \quad \lor \quad x \geq 0 \end{cases}$

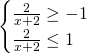
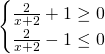
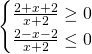
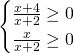
Mettendo a sistema le due soluzioni otteniamo:

$x \leq -4 \quad \lor \quad x \geq 0$

Da cui:

$D: ]-\infty;-4] \quad \cup \quad [0;+\infty[$

(Questa pagina è stata visualizzata da 49 persone)

Matebook