Barbara ci manda la seguente immagine
Risposta dello staff di Matebook
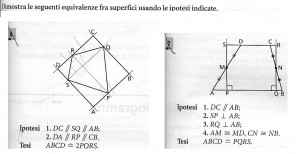
Esercizio 1
Tesi ABCD = 2PQRS
PQRS rappresenta un quadrilatero la cui area si calcola moltiplicando le perpendicolari e dividendo il risultato per 2 (rombo per esattezza)
Ora come si può notare dalle ipotesi le perpendicolari RP e QS sono parallele tra loro rispetto ai lati esterni del rettangolo ABCD da cui deriva la tesi secondo cui l’area di ABCD è esattamente pari al doppio dell’area del rombo inscritto
Esercizio 2
Tesi ABCD = PQRS
Calcoliamo l’area di ABCD. Essendo un trapezio l’area si calcola come somma delle basi per altezza diviso 2. Da cui
ABCD=(AB+CD)*SP/2
i triangoli AMP e MSD sono uguali dal momento che sono simili con un lato uguale.
Sono simili dal momento che gli angoli in M sono alterni interni e quindi uguali e sono entrambi rettangoli.
Essendo uguali i lati DS e AP sono uguali rispettivamente.
Discorso analogo va fatto per i triangoli NCR e NQB. I lati QB e CR sono uguali come sopra.
Ora l’area di PQRS è graficamente pari all’area di ABCD-AMP+DSM-NQB+NCR.
Ma banalmente si tratta di aggiungere e sottrarre aree di triangoli uguali.
(Questa pagina è stata visualizzata da 254 persone)