Esercizio 20 Problemi sui teoremi di Euclide

-4

Traccia

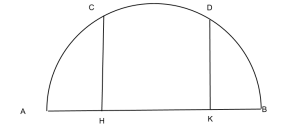
E’ data una semicirconferenza di diametro AB=25 cm e sul diametro AB due punti H e K tali che AH=9 cm e BK=8 cm. Da H e K si conducono le perpendicolari al diametro che incontrano rispettivamente in C e in D la semicirconferenza. Determinare CH,AC,BD,BC,AD.

Svolgimento

Semicirconferenza

Per il secondo teorema di euclide abbiamo che CH^2=AH \cdot HB

AH=9 \mbox{ cm}

BH=AB-AH=(25-9) \mbox{ cm}=16 \mbox{ cm}

Quindi

CH=\sqrt {9 \cdot 16} \mbox{ cm} = \sqrt {144} \mbox{ cm} = 12 \mbox{ cm}

 

Consideriamo il triangolo ACH. Esso è rettangolo in H e sono noti i lati AH e CH.

Applichiamo pitagora per trovare AC

AC=\sqrt {AH^2 + CH^2} = \sqrt {81+144} \mbox{ cm}= \sqrt {225} \mbox{ cm} = 15 \mbox{ cm}

 

Discorso analogo va fatto per DB

DH=\sqrt{AK \cdot KB} =\sqrt {8 \cdot (25-8)} \mbox{ cm}= \sqrt{136} \mbox{ cm}

DB=\sqrt { 136+64} \mbox{ cm} = 10\sqrt 2 \mbox{ cm}

 

Per calcolare BC dobbiamo considerare il triangolo rettangolo ABC rettangolo per definizione in C di cui conosciamo 2 lati.

BC=\sqrt{AB^2-AC^2} = \sqrt{625-225} \mbox{ cm}= \sqrt{400} \mbox{ cm}= 20 \mbox{ cm}

 

Per calcolare AD dobbiamo considerare il triangolo rettangolo ABD rettangolo per definizione in D di cui conosciamo 2 lati.

AD=\sqrt{AB^2-BD^2} = \sqrt{625-200} \mbox{ cm}= \sqrt{425} \mbox{ cm} = 5\sqrt{17} \mbox{ cm}

 

 

 

Altri esercizi simili

(Questa pagina è stata visualizzata da 590 persone)

Lascia un commento