Uno studente scrive:
Oggetto: Equazioni di grado superiore al secondo
Corpo del messaggio:
a)![]()
b) ![]()
c) ![]()
Risposta dello staff
a) Per svolgere questa equazione, utilizziamo la legge di annullamento del prodotto, e quindi analizziamo i due prodotti singolarmente, magari dopo averla scomposta ulteriormente:
![]()
e
![]()
Quindi avremo:
![]()
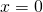
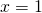
 non ammetterà soluzioni poichè il
non ammetterà soluzioni poichè il 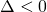
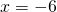
b) Per capire meglio questa è necessario svolgere prima i calcoli:
![]()
![]()
![]()
![]()
Questa ammetterà un’unica soluzione:
![]()
c) Per capire meglio questa è necessario svolgere prima i calcoli:
![]()
![]()
![]()
Utilizziamo Ruffini per scomporre e otteniamo:
| 2 | -3 | -8 | 12 | |
| 2 | 4 | 2 | -12 | |
| 2 | 1 | -6 | 0 |
da cui
![]()
![]()
Quindi ammetterà come soluzioni:
(Questa pagina è stata visualizzata da 174 persone)