Traccia
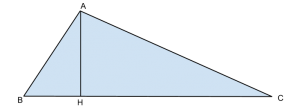
Un triangolo rettangolo ABC ha l’ipotenusa BC di 60 cm ed è 4AC=3AB.Determinare perimetro e area di un triangolo simile il cui cateto minore è 64 cm.
Svolgimento
Poniamo ![]() ,
,
così da trovare l’incognita sfruttando il teorema di Pitagora: ![]() ,
,
sapendo che:
![]() :
:
![]()
![]()
![]()
![]()
da qui avremo:
![]()
![]()
Per il criterio di similitudine, senza bisogno di calcolare tutti i lati del triangolo simile possiamo calcolare perimetro e area, sapendo che:
![]()
e
![]() .
.
Ora possiamo trovare il perimetro e l’area del triangolo simile sfruttando le proporzioni sul cateto minore:
![]()
![]()
![]()
mentre per l’area bisognerà considerare il rapporto dei quadrati:
![]()
![]()
![]()
Altri esercizi simili:
- Esercizio 1 Problemi su triangoli e poligoni simili
- Esercizio 2 Problemi su triangoli e poligoni simili
- Esercizio 3 Problemi su triangoli e poligoni simili
- Esercizio 4 Problemi su triangoli e poligoni simili
- Esercizio 5 Problemi su triangoli e poligoni simili
- Esercizio 6 Problemi su triangoli e poligoni simili
- Esercizio 7 Problemi su triangoli e poligoni simili
- Esercizio 8 Problemi su triangoli e poligoni simili
- Esercizio 9 Problemi su triangoli e poligoni simili
- Esercizio 10 Problemi su triangoli e poligoni simili
- Esercizio 11 Problemi su triangoli e poligoni simili
- Esercizio 12 Problemi su triangoli e poligoni simili
- Esercizio 13 Problemi su triangoli e poligoni simili
- Esercizio 14 Problemi su triangoli e poligoni simili
- Esercizio 15 Problemi su triangoli e poligoni simili
- Esercizio 16 Problemi su triangoli e poligoni simili
- Esercizio 17 Problemi su triangoli e poligoni simili
- Esercizio 18 Problemi su triangoli e poligoni simili
- Esercizio 19 Problemi su triangoli e poligoni simili
- Esercizio 20 Problemi su triangoli e poligoni simili
- Esercizio 21 Problemi su triangoli e poligoni simili
- Esercizio 22 Problemi su triangoli e poligoni simili
- Esercizio 23 Problemi su triangoli e poligoni simili
- Esercizio 24 Problemi su triangoli e poligoni simili
- Esercizio 25 Problemi su triangoli e poligoni simili
- Esercizio 26 Problemi su triangoli e poligoni simili
- Esercizio 27 Problemi su triangoli e poligoni simili
- Esercizio 28 Problemi su triangoli e poligoni simili
- Esercizio 29 Problemi su triangoli e poligoni simili
- Esercizio 30 Problemi su triangoli e poligoni simili
(Questa pagina è stata visualizzata da 199 persone)