Esercizio 26 Problemi su triangoli e poligoni simili

-5

Traccia

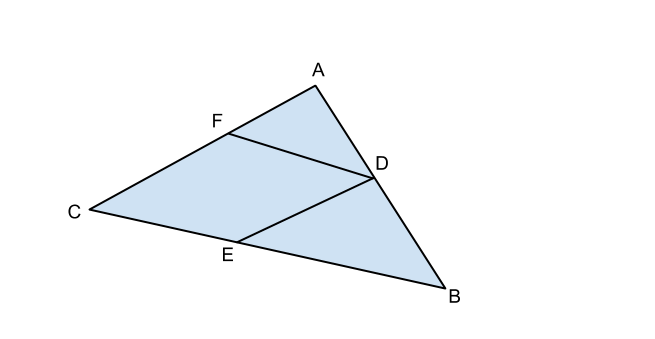
Nel triangolo ABC i lati AB,BC e AC misurano rispettivamente 5a,7a e 4a. Determinare sul lato AB un punto D tale che, conducendo la corda DE parallela ad AC e la corda DF parallela a BC, il parallelogrammo DECF risulti un rombo.

Svolgimento

 

triangolo con corde

Ricordiamo che, per essere un rombo, DECF deve avere tutti e quattro i lati uguali.

Per adesso sappiamo per certo che i lati opposti sono uguali perchè per costruzione DECF è un parallelogrammo.

Poniamo quindi:

DE=CF=DF=EC=x.

Notiamo che i triangoli BED e ADF sono simili e quindi:

DF:BE=AF:DE

\frac {x}{7a-x}=\frac {4a-x}{x}

x^2=28a^2-7ax-4ax+x^2

11ax=28a^2

x=\frac {28}{11}a

E quindi il lato del rombo sarà:

DE=\frac {28}{11}a.

 

 

 

 

 

Altri esercizi simili:

 

 

(Questa pagina è stata visualizzata da 111 persone)

Un pensiero riguardo “Esercizio 26 Problemi su triangoli e poligoni simili”

Lascia un commento