Esercizio 28 Problemi su triangoli e poligoni simili

-1

Traccia

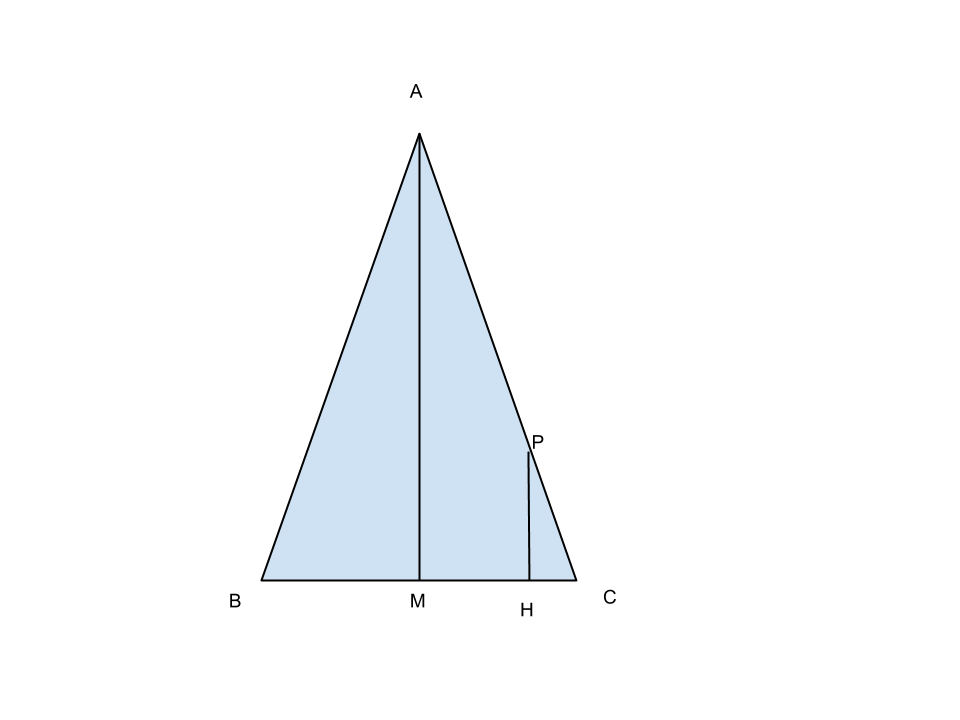
Si considera un triangolo isoscele ABC di base BC=2a e lato AB=3a. Determinare un punto P sul lato AC in modo che, detta H la sua proiezione su BC, si abbia PC^2+BH^2=4a^2. In corrispondenza al punto P che è soluzione del problema si calcoli la misura di BP.

Svolgimento

isoscele con proiezione

Per riuscire a risolvere il problema tracciamo l’altezza AM ; notiamo che i triangoli AMC e PHC sono simili e quindi:

PC:AC=CH:CM

Poniamo CH=x, e otteniamo:

PC=\frac {AC \cdot CH}{CM}=\frac {3ax}{a}=3x

Otteniamo BH come differenza di lati:

BH=BC-CH=2a-x

Risolviamo ora il problema:

PC^2+BH^2=4a^2

9x^2 + 4a^2-4ax+x^2=4a^2

10x^2-4ax=0

x(10x-4a)=0

Supponendo che un lato non possa mai essere uguale a 0, otteniamo che:

x=\frac {2}{5}a

Ora, per calcolare BP useremo il teorema di Pitagora su BPH, sapendo che:

BH=2a-x=\frac {8}{5}a

PC=\frac {6}{5}a

PH^2=PC^2-CH^2=\frac {36}{25}a^2-\frac {4}{25}a^2=\frac {32}{25}a^2

BP=\sqrt {BH^2+PH^2}=\sqrt{\frac {64}{25}+\frac {32}{25}}a=\sqrt{\frac {96}{25}}a=\frac 45a \sqrt 6


 

 

 

Altri esercizi simili:

 

 

(Questa pagina è stata visualizzata da 90 persone)

Lascia un commento