Esercizio 29 Problemi su triangoli e poligoni simili

0

Traccia

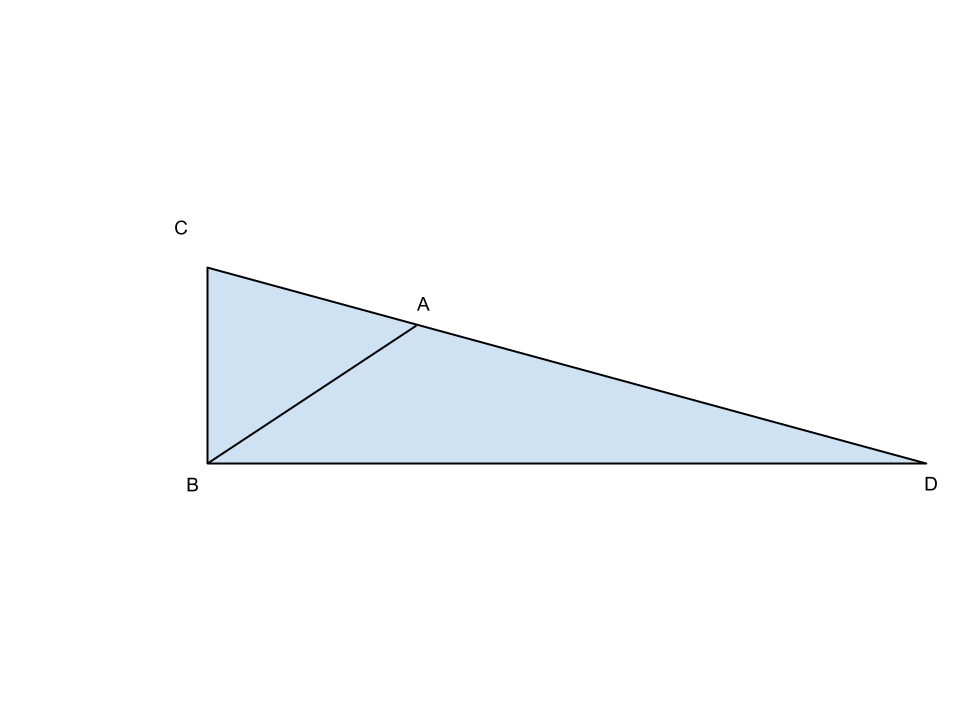
Nel  triangolo isoscele ABC, di base AB, la perpendicolare al lato BC, condotta per B, incontra il prolungamento del lato AC in D e si sa che il segmento BD è doppio del segmento AD. Determinare le lunghezze dei cateti del triangolo rettangolo CBD e della base del triangolo isoscele sapendo che l’area del triangolo CDB è 24 cm^2.

Svolgimento

triangolo isoscele acutangolo (1)

Dai dati e dalla costruzione poniamo AD=x, e AC=BC=y, e avremo:

BD=2x.

Da qui sappiamo che:

A_{CBD}=\frac 12 (BD \cdot BC)=xy=24 \mbox { cm}^2.

Ma si nota anche che:

CD=AC+AD=x+y.

Per trovare le incognite svolgiamo il sistema:

\begin{cases} xy=24 \\ (x+y)^2=4x^2+y^2\end{cases}

\begin{cases} xy=24 \\ x^2+2xy+y^2=4x^2+y^2\end{cases}

\begin{cases} xy=24 \\ x^2+48=4x^2\end{cases}

\begin{cases} xy=24 \\ 3x^2=48\end{cases}

\begin{cases} xy=24 \\ x^2=16\end{cases}

\begin{cases} xy=24 \\ x=4 \end{cases}

\begin{cases} y=6 \\ x=4\end{cases}.

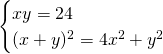
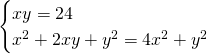
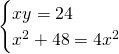
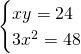
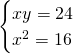
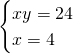
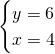Quindi avremo che:

BD=2x=8 \mbox { cm}

CB=6 \mbox { cm}.

Per trovare AB tracciamo l’altezza BH del triangolo BCD,e sfruttiamo Euclide:

CH=\frac {CB^2}{CD}=\frac {36}{10}\mbox { cm}=3,6 \mbox { cm}.

AH=AC-CH=2,4 \mbox { cm}.

HD=6,4 \mbox { cm}.

BH=\sqrt {CH \cdot HD}=\sqrt {3,6 \cdot 6,4}\mbox { cm}=4,8 \mbox { cm}.

Ricaviamo AB con il teorema di Pitagora:

AB=\sqrt {BH^2+AH^2}=\sqrt{(\frac {24}{5})^2 + (\frac {12}{5})^2}\mbox { cm}=\sqrt {\frac {576}{25}+\frac {144}{25}}\mbox { cm}=\sqrt {\frac {720}{25}}\mbox{ cm}=\frac {12}{5}\sqrt 5 \mbox { cm}

 

 

 

 

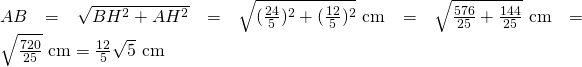
Altri esercizi simili:

 

 

(Questa pagina è stata visualizzata da 78 persone)

Lascia un commento