Corpo del messaggio:
ciao questo e l’esercizio: integrale di dx fratto la radice di e ^2x+2e^x .
mandami la soluzione alla mia email.
Risposta dello staff
![]()
Imponiamo la sostituzione:
![]()
![]()
![]()
Sostituendo nell’integrale iniziale otteniamo:
![]()
![]()
Utilizziamo il criterio di integrazione per le funzioni razionali:
![]()
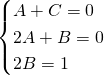
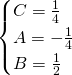 .
.
Quindi l’integrale diventerà:
![]()
![]()
![]()
![]()
![]()
(Questa pagina è stata visualizzata da 190 persone)