Oggetto: soluzione di un esercizio
Corpo del messaggio:
ciao come si risolve questo integrale:dx fratto la radice di e^2x+2e^x grazie ciaooo
![]()
Effettuiamo una sostituzione:
![]()
![]()
![]() .
.
L’integrale diventa così:
![]()
![]() .
.
Da qui avremo:
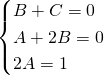
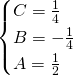 .
.
L’integrale quindi diventa:
![]()
![]()
![]()
![]()
(Questa pagina è stata visualizzata da 134 persone)